Quick and energy-efficient Bayesian computing of binocular disparity using stochastic digital signals

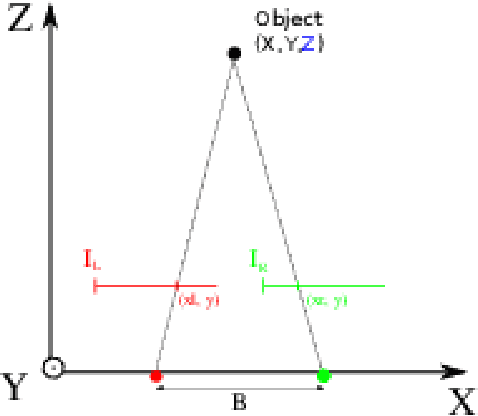
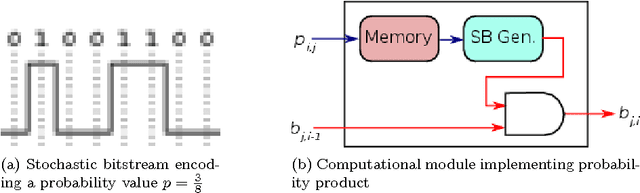
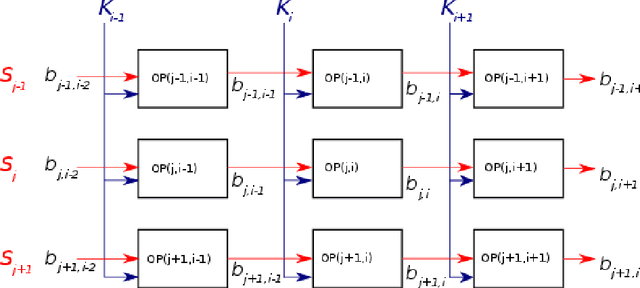
Reconstruction of the tridimensional geometry of a visual scene using the binocular disparity information is an important issue in computer vision and mobile robotics, which can be formulated as a Bayesian inference problem. However, computation of the full disparity distribution with an advanced Bayesian model is usually an intractable problem, and proves computationally challenging even with a simple model. In this paper, we show how probabilistic hardware using distributed memory and alternate representation of data as stochastic bitstreams can solve that problem with high performance and energy efficiency. We put forward a way to express discrete probability distributions using stochastic data representations and perform Bayesian fusion using those representations, and show how that approach can be applied to diparity computation. We evaluate the system using a simulated stochastic implementation and discuss possible hardware implementations of such architectures and their potential for sensorimotor processing and robotics.

Toward Biochemical Probabilistic Computation

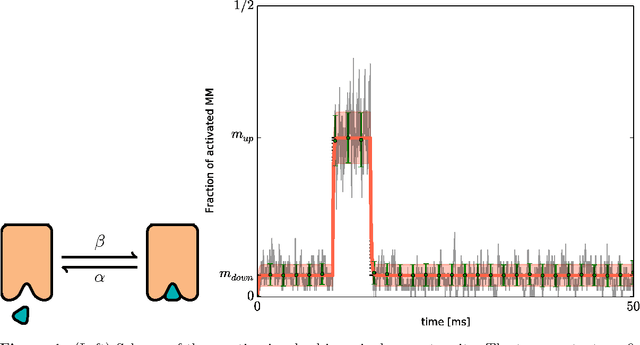
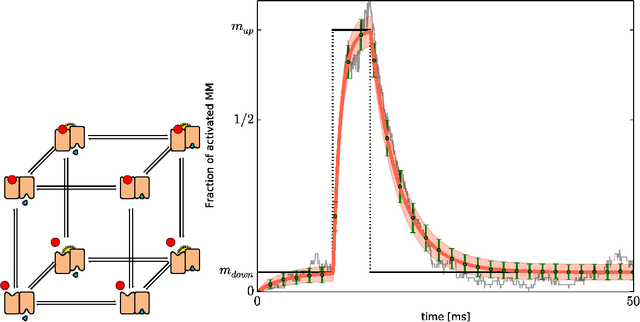
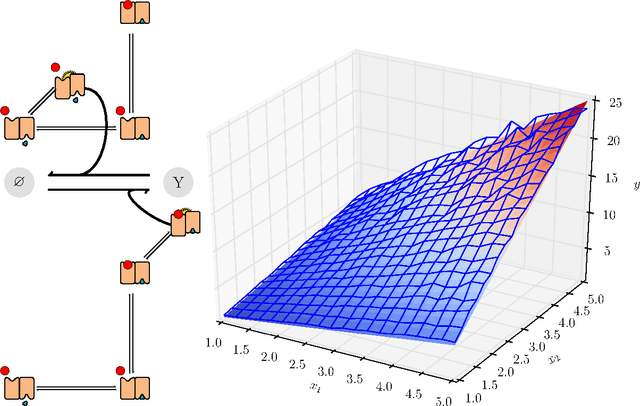
Living organisms survive and multiply even though they have uncertain and incomplete information about their environment and imperfect models to predict the consequences of their actions. Bayesian models have been proposed to face this challenge. Indeed, Bayesian inference is a way to do optimal reasoning when only uncertain and incomplete information is available. Various perceptive, sensory-motor, and cognitive functions have been successfully modeled this way. However, the biological mechanisms allowing animals and humans to represent and to compute probability distributions are not known. It has been proposed that neurons and assemblies of neurons could be the appropriate scale to search for clues to probabilistic reasoning. In contrast, in this paper, we propose that interacting populations of macromolecules and diffusible messengers can perform probabilistic computation. This suggests that probabilistic reasoning, based on cellular signaling pathways, is a fundamental skill of living organisms available to the simplest unicellular organisms as well as the most complex brains.

Decision Making under Uncertainty: A Quasimetric Approach

We propose a new approach for solving a class of discrete decision making problems under uncertainty with positive cost. This issue concerns multiple and diverse fields such as engineering, economics, artificial intelligence, cognitive science and many others. Basically, an agent has to choose a single or series of actions from a set of options, without knowing for sure their consequences. Schematically, two main approaches have been followed: either the agent learns which option is the correct one to choose in a given situation by trial and error, or the agent already has some knowledge on the possible consequences of his decisions; this knowledge being generally expressed as a conditional probability distribution. In the latter case, several optimal or suboptimal methods have been proposed to exploit this uncertain knowledge in various contexts. In this work, we propose following a different approach, based on the geometric intuition of distance. More precisely, we define a goal independent quasimetric structure on the state space, taking into account both cost function and transition probability. We then compare precision and computation time with classical approaches.