Supervised segmentation of NO2 plumes from individual ships using TROPOMI satellite data

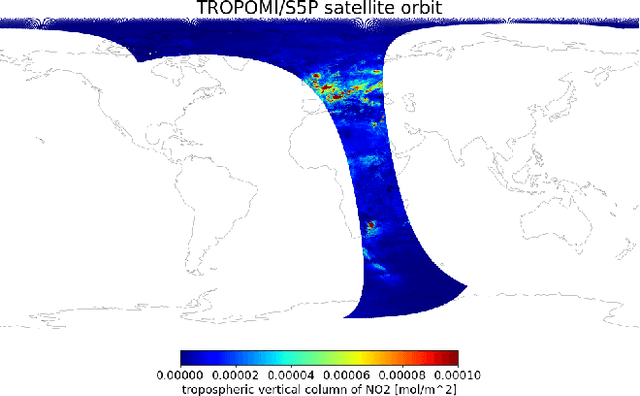
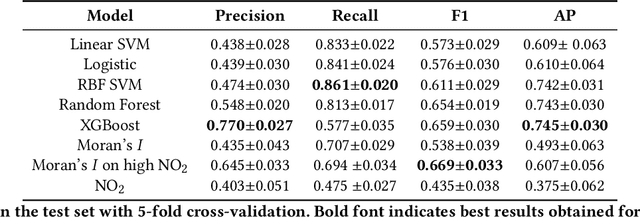
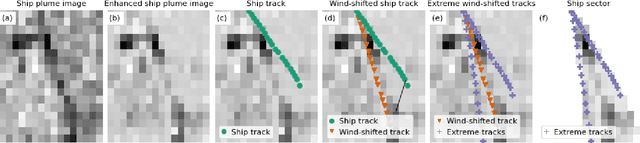
Starting from 2021, the International Maritime Organization significantly tightened the $\text{NO}_\text{x}$ emission requirements for ships entering the Baltic and North Sea waters. Since all methods currently used for the ships' compliance monitoring are costly and require proximity to the ship, the performance of a global and continuous monitoring of the emission standards' fulfillment has been impossible up to now. A promising approach is the use of remote sensing with the recently launched TROPOMI/S5P satellite. Due to its unprecedentedly high spatial resolution, it allows for the visual distinction of $\text{NO}_\text{2}$ plumes of individual ships. To successfully deploy a compliance monitoring system that is based on TROPOMI data, an automated procedure for the attribution of $\text{NO}_\text{2}$ to individual ships has to be developed. However, due to the extremely low signal-to-noise ratio, interference with the signal from other - often stronger - sources, and the absence of ground truth, the task is very challenging. In this study, we present an automated method for segmentation of plumes produced by individual ships using TROPOMI satellite data - a first step towards the automated procedure for global ship compliance monitoring. We develop a multivariate plume segmentation method based on various ships', wind's and spatial properties. For this, we propose to automatically define a region of interest - a ship sector that we normalize with respect to scale and orientation. We create a dataset, where each pixel has a label for belonging to the respective ship plume or not. We train five linear and nonlinear classifiers. The results show a significant improvement over the threshold-based baselines. Moreover, the aggregated $\text{NO}_\text{2}$ levels of the segmented plumes show high correlation with the theoretically derived measure of ship's emission potential.

ROS Regression: Integrating Regularization and Optimal Scaling Regression

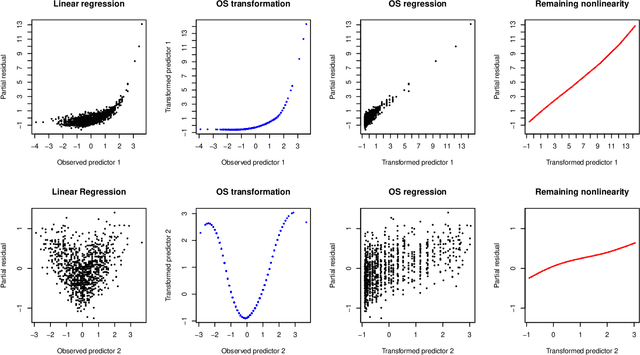
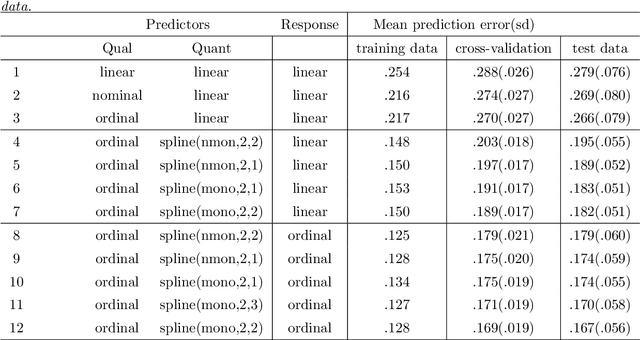
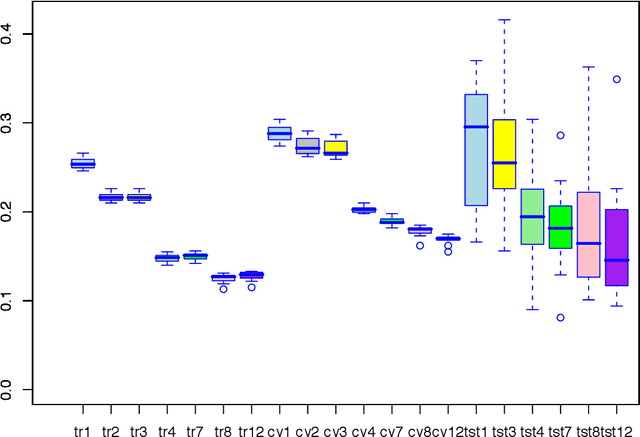
In this paper we combine two important extensions of ordinary least squares regression: regularization and optimal scaling. Optimal scaling (sometimes also called optimal scoring) has originally been developed for categorical data, and the process finds quantifications for the categories that are optimal for the regression model in the sense that they maximize the multiple correlation. Although the optimal scaling method was developed initially for variables with a limited number of categories, optimal transformations of continuous variables are a special case. We will consider a variety of transformation types; typically we use step functions for categorical variables, and smooth (spline) functions for continuous variables. Both types of functions can be restricted to be monotonic, preserving the ordinal information in the data. In addition to optimal scaling, three regularization methods will be considered: Ridge regression, the Lasso, and the Elastic Net. The resulting method will be called ROS Regression (Regularized Optimal Scaling Regression. We will show that the basic OS algorithm provides straightforward and efficient estimation of the regularized regression coefficients, automatically gives the Group Lasso and Blockwise Sparse Regression, and extends them with monotonicity properties. We will show that Optimal Scaling linearizes nonlinear relationships between predictors and outcome, and improves upon the condition of the predictor correlation matrix, increasing (on average) the conditional independence of the predictors. Alternative options for regularization of either regression coefficients or category quantifications are mentioned. Extended examples are provided. Keywords: Categorical Data, Optimal Scaling, Conditional Independence, Step Functions, Splines, Monotonic Transformations, Regularization, Lasso, Elastic Net, Group Lasso, Blockwise Sparse Regression.