Jacob Ouanounou
Learning K-U-Net with constant complexity: An Application to time series forecasting
Oct 03, 2024



Abstract:Training deep models for time series forecasting is a critical task with an inherent challenge of time complexity. While current methods generally ensure linear time complexity, our observations on temporal redundancy show that high-level features are learned 98.44\% slower than low-level features. To address this issue, we introduce a new exponentially weighted stochastic gradient descent algorithm designed to achieve constant time complexity in deep learning models. We prove that the theoretical complexity of this learning method is constant. Evaluation of this method on Kernel U-Net (K-U-Net) on synthetic datasets shows a significant reduction in complexity while improving the accuracy of the test set.
Anomaly Prediction: A Novel Approach with Explicit Delay and Horizon
Aug 09, 2024



Abstract:Anomaly detection in time series data is a critical challenge across various domains. Traditional methods typically focus on identifying anomalies in immediate subsequent steps, often underestimating the significance of temporal dynamics such as delay time and horizons of anomalies, which generally require extensive post-analysis. This paper introduces a novel approach for detecting time series anomalies called Anomaly Prediction, incorporating temporal information directly into the prediction results. We propose a new dataset specifically designed to evaluate this approach and conduct comprehensive experiments using several state-of-the-art time series forecasting methods. The results demonstrate the efficacy of our approach in providing timely and accurate anomaly predictions, setting a new benchmark for future research in this field.
Robust Time Series Forecasting with Non-Heavy-Tailed Gaussian Loss-Weighted Sampler
Jun 19, 2024



Abstract:Forecasting multivariate time series is a computationally intensive task challenged by extreme or redundant samples. Recent resampling methods aim to increase training efficiency by reweighting samples based on their running losses. However, these methods do not solve the problems caused by heavy-tailed distribution losses, such as overfitting to outliers. To tackle these issues, we introduce a novel approach: a Gaussian loss-weighted sampler that multiplies their running losses with a Gaussian distribution weight. It reduces the probability of selecting samples with very low or very high losses while favoring those close to average losses. As it creates a weighted loss distribution that is not heavy-tailed theoretically, there are several advantages to highlight compared to existing methods: 1) it relieves the inefficiency in learning redundant easy samples and overfitting to outliers, 2) It improves training efficiency by preferentially learning samples close to the average loss. Application on real-world time series forecasting datasets demonstrate improvements in prediction quality for 1%-4% using mean square error measurements in channel-independent settings. The code will be available online after 1 the review.
Kernel-U-Net: Hierarchical and Symmetrical Framework for Multivariate Time Series Forecasting
Jan 03, 2024
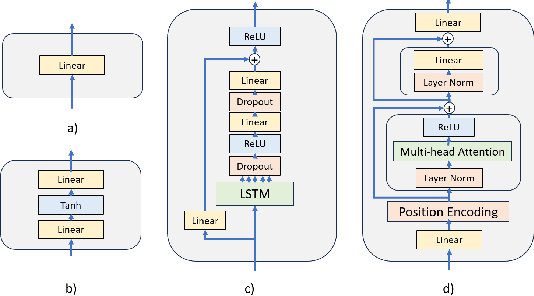
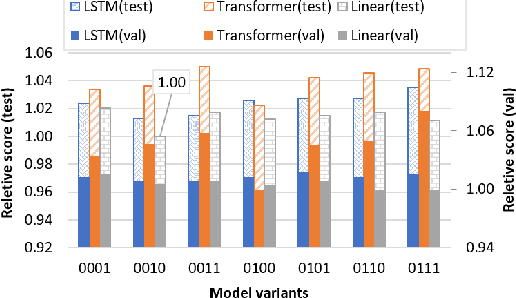
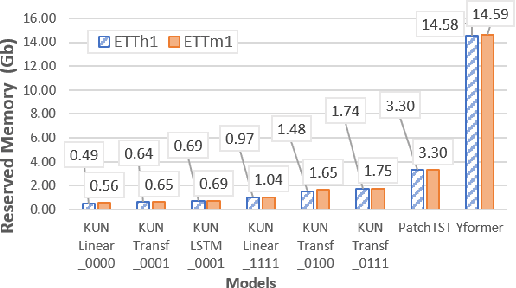
Abstract:Time series forecasting task predicts future trends based on historical information. Recent U-Net-based methods have demonstrated superior performance in predicting real-world datasets. However, the performance of these models is lower than patch-based models or linear models. In this work, we propose a symmetric and hierarchical framework, Kernel-U-Net, which cuts the input sequence into slices at each layer of the network and then computes them using kernels. Furthermore, it generalizes the concept of convolutional kernels in classic U-Net to accept custom kernels that follow the same design pattern. Compared to the existing linear or transformer-based solution, our model contains 3 advantages: 1) A small number of parameters: the parameters size is $O(log(L)^2)$ where $L$ is the look-back window size, 2) Flexibility: its kernels can be customized and fitted to the datasets, 3) Computation efficiency: the computation complexity of transformer modules is reduced to $O(log(L)^2)$ if they are placed close to the latent vector. Kernel-U-Net accuracy was greater than or equal to the state-of-the-art model on six (out of seven) real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge