Kernel-U-Net: Hierarchical and Symmetrical Framework for Multivariate Time Series Forecasting
Paper and Code
Jan 03, 2024
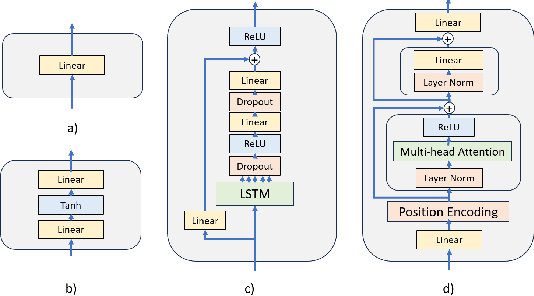
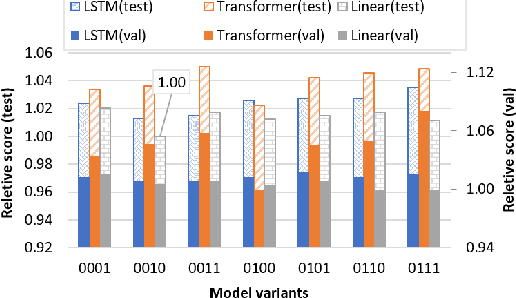
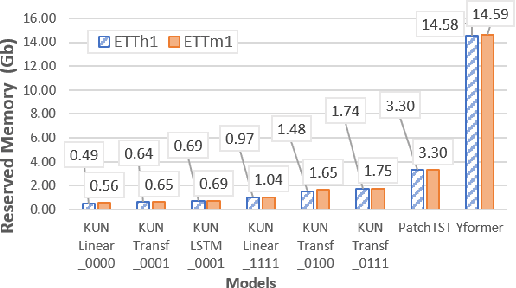
Time series forecasting task predicts future trends based on historical information. Recent U-Net-based methods have demonstrated superior performance in predicting real-world datasets. However, the performance of these models is lower than patch-based models or linear models. In this work, we propose a symmetric and hierarchical framework, Kernel-U-Net, which cuts the input sequence into slices at each layer of the network and then computes them using kernels. Furthermore, it generalizes the concept of convolutional kernels in classic U-Net to accept custom kernels that follow the same design pattern. Compared to the existing linear or transformer-based solution, our model contains 3 advantages: 1) A small number of parameters: the parameters size is $O(log(L)^2)$ where $L$ is the look-back window size, 2) Flexibility: its kernels can be customized and fitted to the datasets, 3) Computation efficiency: the computation complexity of transformer modules is reduced to $O(log(L)^2)$ if they are placed close to the latent vector. Kernel-U-Net accuracy was greater than or equal to the state-of-the-art model on six (out of seven) real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge