A Zero-Shot Learning Approach for Ephemeral Gully Detection from Remote Sensing using Vision Language Models

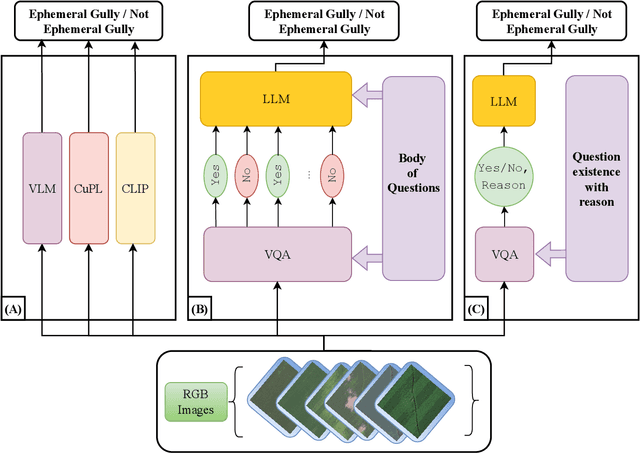
Ephemeral gullies are a primary cause of soil erosion and their reliable, accurate, and early detection will facilitate significant improvements in the sustainability of global agricultural systems. In our view, prior research has not successfully addressed automated detection of ephemeral gullies from remotely sensed images, so for the first time, we present and evaluate three successful pipelines for ephemeral gully detection. Our pipelines utilize remotely sensed images, acquired from specific agricultural areas over a period of time. The pipelines were tested with various choices of Visual Language Models (VLMs), and they classified the images based on the presence of ephemeral gullies with accuracy higher than 70% and a F1-score close to 80% for positive gully detection. Additionally, we developed the first public dataset for ephemeral gully detection, labeled by a team of soil- and plant-science experts. To evaluate the proposed pipelines, we employed a variety of zero-shot classification methods based on State-of-the-Art (SOTA) open-source Vision-Language Models (VLMs). In addition to that, we compare the same pipelines with a transfer learning approach. Extensive experiments were conducted to validate the detection pipelines and to analyze the impact of hyperparameter changes in their performance. The experimental results demonstrate that the proposed zero-shot classification pipelines are highly effective in detecting ephemeral gullies in a scenario where classification datasets are scarce.

Achieving Unit-Consistent Pseudo-Inverse-based Path-Planning for Redundant Incommensurate Robotic Manipulators

In this paper, we review and compare several velocity-level and acceleration-level Pseudo-Inverse-based Path Planning (PPP) and Pseudo-Inverse-based Repetitive Motion Planning (PRMP) schemes based on the kinematic model of robotic manipulators. We show that without unit consistency in the pseudo-inverse computation, path planning of incommensurate robotic manipulators will fail. Also, we investigated the robustness and noise tolerance of six PPP and PRMP schemes in the literature against various noise types (i.e. zero, constant, time-varying and random noises). We compared the simulated results using two redundant robotic manipulators: a 3DoF (2RP), and a 7DoF (2RP4R). These experimental results demonstrate that the improper Generalized Inverse (GI) with arbitrary selection of unit and/or in the presence of noise can lead to unexpected behavior of the robot, while producing wrong instantaneous outputs in the task space, which results in distortions and/or failures in the execution of the planned path. Finally, we propose and demonstrate the efficacy of the Mixed Inverse (MX) as the proper GI to achieve unit-consistency in path planning.

Choosing the Correct Generalized Inverse for the Numerical Solution of the Inverse Kinematics of Incommensurate Robotic Manipulators

Numerical methods for Inverse Kinematics (IK) employ iterative, linear approximations of the IK until the end-effector is brought from its initial pose to the desired final pose. These methods require the computation of the Jacobian of the Forward Kinematics (FK) and its inverse in the linear approximation of the IK. Despite all the successful implementations reported in the literature, Jacobian-based IK methods can still fail to preserve certain useful properties if an improper matrix inverse, e.g. Moore-Penrose (MP), is employed for incommensurate robotic systems. In this paper, we propose a systematic, robust and accurate numerical solution for the IK problem using the Mixed (MX) Generalized Inverse (GI) applied to any type of Jacobians (e.g., analytical, numerical or geometric) derived for any commensurate and incommensurate robot. This approach is robust to whether the system is under-determined (less than 6 DoF) or over-determined (more than 6 DoF). We investigate six robotics manipulators with various Degrees of Freedom (DoF) to demonstrate that commonly used GI's fail to guarantee the same system behaviors when the units are varied for incommensurate robotics manipulators. In addition, we evaluate the proposed methodology as a global IK solver and compare against well-known IK methods for redundant manipulators. Based on the experimental results, we conclude that the right choice of GI is crucial in preserving certain properties of the system (i.e. unit-consistency).