Reconstructing Sea Surface Temperature Images: A Masked Autoencoder Approach for Cloud Masking and Reconstruction

This thesis presents a new algorithm to mitigate cloud masking in the analysis of sea surface temperature (SST) data generated by remote sensing technologies, e.g., Clouds interfere with the analysis of all remote sensing data using wavelengths shorter than 12 microns, significantly limiting the quantity of usable data and creating a biased geographical distribution (towards equatorial and coastal regions). To address this issue, we propose an unsupervised machine learning algorithm called Enki which uses a Vision Transformer with Masked Autoencoding to reconstruct masked pixels. We train four different models of Enki with varying mask ratios (t) of 10%, 35%, 50%, and 75% on the generated Ocean General Circulation Model (OGCM) dataset referred to as LLC4320. To evaluate performance, we reconstruct a validation set of LLC4320 SST images with random ``clouds'' corrupting p=10%, 20%, 30%, 40%, 50% of the images with individual patches of 4x4 pixel^2. We consistently find that at all levels of p there is one or multiple models that reconstruct the images with a mean RMSE of less than 0.03K, i.e. lower than the estimated sensor error of VIIRS data. Similarly, at the individual patch level, the reconstructions have RMSE 8x smaller than the fluctuations in the patch. And, as anticipated, reconstruction errors are larger for images with a higher degree of complexity. Our analysis also reveals that patches along the image border have systematically higher reconstruction error; we recommend ignoring these in production. We conclude that Enki shows great promise to surpass in-painting as a means of reconstructing cloud masking. Future research will develop Enki to reconstruct real-world data.

Monte Carlo Physarum Machine: Characteristics of Pattern Formation in Continuous Stochastic Transport Networks

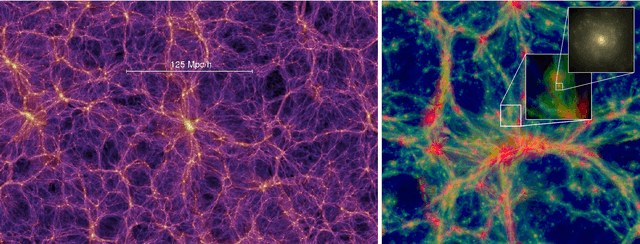
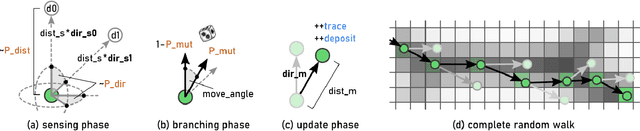
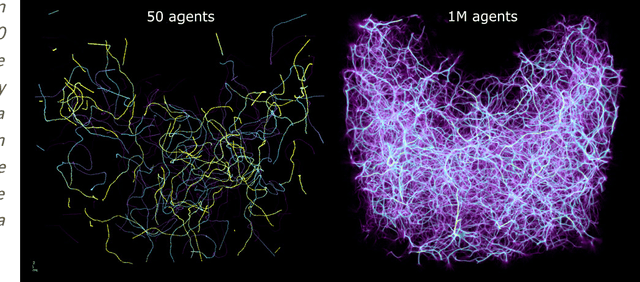
We present Monte Carlo Physarum Machine: a computational model suitable for reconstructing continuous transport networks from sparse 2D and 3D data. MCPM is a probabilistic generalization of Jones's 2010 agent-based model for simulating the growth of Physarum polycephalum slime mold. We compare MCPM to Jones's work on theoretical grounds, and describe a task-specific variant designed for reconstructing the large-scale distribution of gas and dark matter in the Universe known as the Cosmic web. To analyze the new model, we first explore MCPM's self-patterning behavior, showing a wide range of continuous network-like morphologies -- called "polyphorms" -- that the model produces from geometrically intuitive parameters. Applying MCPM to both simulated and observational cosmological datasets, we then evaluate its ability to produce consistent 3D density maps of the Cosmic web. Finally, we examine other possible tasks where MCPM could be useful, along with several examples of fitting to domain-specific data as proofs of concept.

Fully probabilistic quasar continua predictions near Lyman-α with conditional neural spline flows

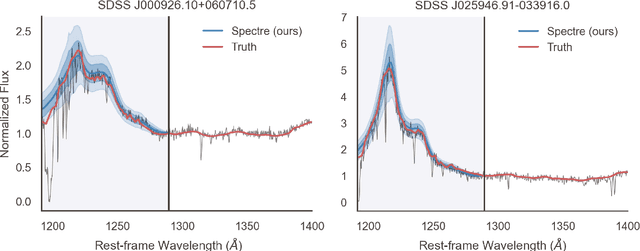
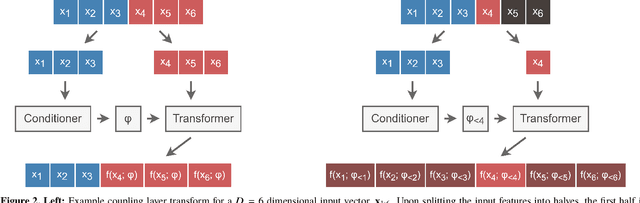
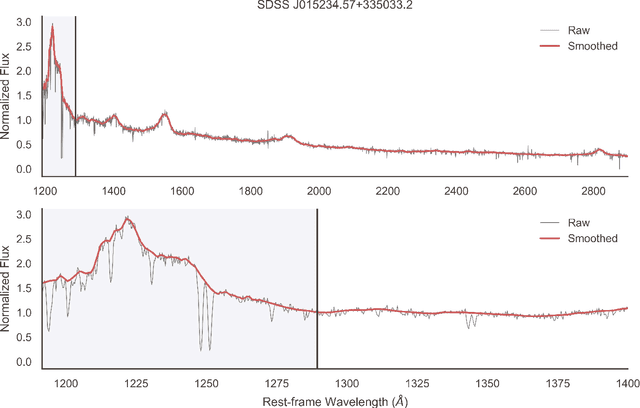
Measurement of the red damping wing of neutral hydrogen in quasar spectra provides a probe of the epoch of reionization in the early Universe. Such quantification requires precise and unbiased estimates of the intrinsic continua near Lyman-$\alpha$ (Ly$\alpha$), a challenging task given the highly variable Ly$\alpha$ emission profiles of quasars. Here, we introduce a fully probabilistic approach to intrinsic continua prediction. We frame the problem as a conditional density estimation task and explicitly model the distribution over plausible blue-side continua ($1190\ \unicode{xC5} \leq \lambda_{\text{rest}} < 1290\ \unicode{xC5}$) conditional on the red-side spectrum ($1290\ \unicode{xC5} \leq \lambda_{\text{rest}} < 2900\ \unicode{xC5}$) using normalizing flows. Our approach achieves state-of-the-art precision and accuracy, allows for sampling one thousand plausible continua in less than a tenth of a second, and can natively provide confidence intervals on the blue-side continua via Monte Carlo sampling. We measure the damping wing effect in two $z>7$ quasars and estimate the volume-averaged neutral fraction of hydrogen from each, finding $\bar{x}_\text{HI}=0.304 \pm 0.042$ for ULAS J1120+0641 ($z=7.09$) and $\bar{x}_\text{HI}=0.384 \pm 0.133$ for ULAS J1342+0928 ($z=7.54$).