Few-shot Image Recognition with Manifolds

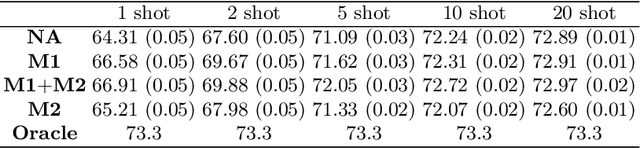
In this paper, we extend the traditional few-shot learning (FSL) problem to the situation when the source-domain data is not accessible but only high-level information in the form of class prototypes is available. This limited information setup for the FSL problem deserves much attention due to its implication of privacy-preserving inaccessibility to the source-domain data but it has rarely been addressed before. Because of limited training data, we propose a non-parametric approach to this FSL problem by assuming that all the class prototypes are structurally arranged on a manifold. Accordingly, we estimate the novel-class prototype locations by projecting the few-shot samples onto the average of the subspaces on which the surrounding classes lie. During classification, we again exploit the structural arrangement of the categories by inducing a Markov chain on the graph constructed with the class prototypes. This manifold distance obtained using the Markov chain is expected to produce better results compared to a traditional nearest-neighbor-based Euclidean distance. To evaluate our proposed framework, we have tested it on two image datasets - the large-scale ImageNet and the small-scale but fine-grained CUB-200. We have also studied parameter sensitivity to better understand our framework.

Multi-step Online Unsupervised Domain Adaptation

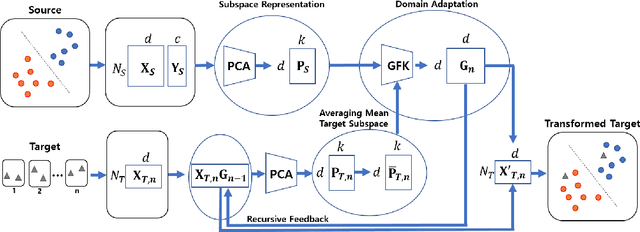
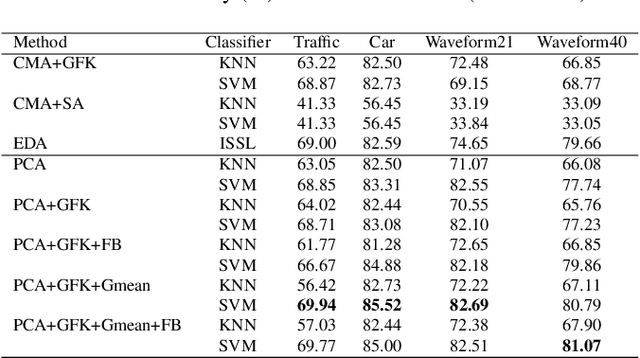
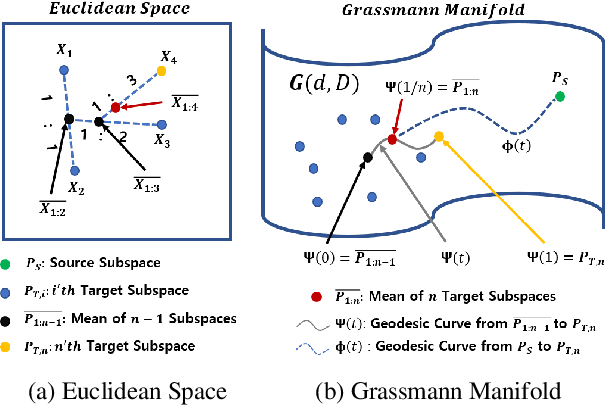
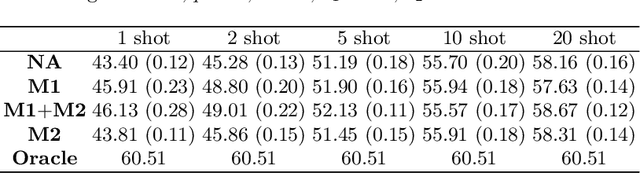
In this paper, we address the Online Unsupervised Domain Adaptation (OUDA) problem, where the target data are unlabelled and arriving sequentially. The traditional methods on the OUDA problem mainly focus on transforming each arriving target data to the source domain, and they do not sufficiently consider the temporal coherency and accumulative statistics among the arriving target data. We propose a multi-step framework for the OUDA problem, which institutes a novel method to compute the mean-target subspace inspired by the geometrical interpretation on the Euclidean space. This mean-target subspace contains accumulative temporal information among the arrived target data. Moreover, the transformation matrix computed from the mean-target subspace is applied to the next target data as a preprocessing step, aligning the target data closer to the source domain. Experiments on four datasets demonstrated the contribution of each step in our proposed multi-step OUDA framework and its performance over previous approaches.