The Topological Fusion of Bayes Nets

Bayes nets are relatively recent innovations. As a result, most of their theoretical development has focused on the simplest class of single-author models. The introduction of more sophisticated multiple-author settings raises a variety of interesting questions. One such question involves the nature of compromise and consensus. Posterior compromises let each model process all data to arrive at an independent response, and then split the difference. Prior compromises, on the other hand, force compromise to be reached on all points before data is observed. This paper introduces prior compromises in a Bayes net setting. It outlines the problem and develops an efficient algorithm for fusing two directed acyclic graphs into a single, consensus structure, which may then be used as the basis of a prior compromise.

Deriving a Minimal I-map of a Belief Network Relative to a Target Ordering of its Nodes

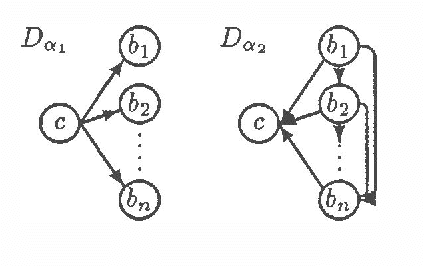
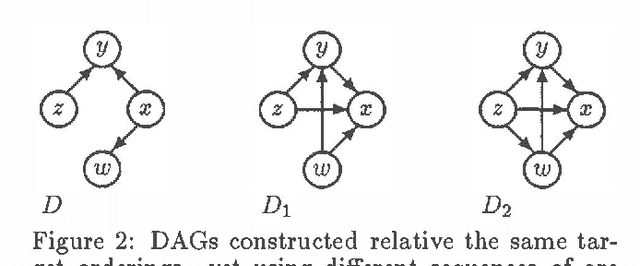
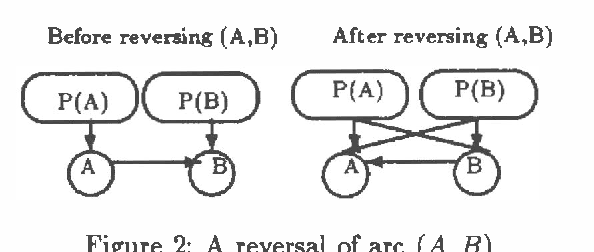
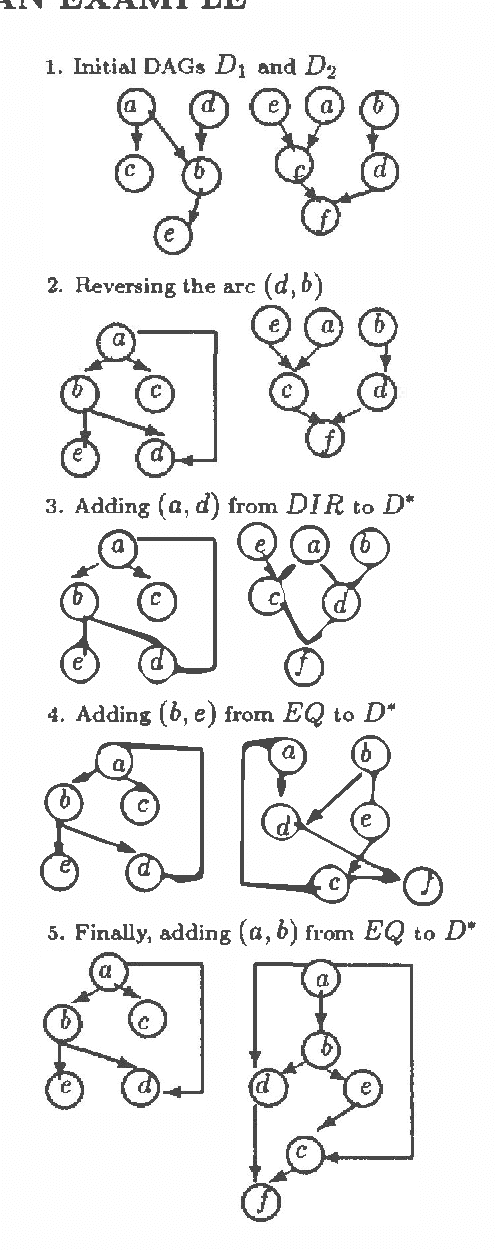
This paper identifies and solves a new optimization problem: Given a belief network (BN) and a target ordering on its variables, how can we efficiently derive its minimal I-map whose arcs are consistent with the target ordering? We present three solutions to this problem, all of which lead to directed acyclic graphs based on the original BN's recursive basis relative to the specified ordering (such a DAG is sometimes termed the boundary DAG drawn from the given BN relative to the said ordering [5]). Along the way, we also uncover an important general principal about arc reversals: when reordering a BN according to some target ordering, (while attempting to minimize the number of arcs generated), the sequence of arc reversals should follow the topological ordering induced by the original belief network's arcs to as great an extent as possible. These results promise to have a significant impact on the derivation of consensus models, as well as on other algorithms that require the reconfiguration and/or combination of BN's.

Some Complexity Considerations in the Combination of Belief Networks

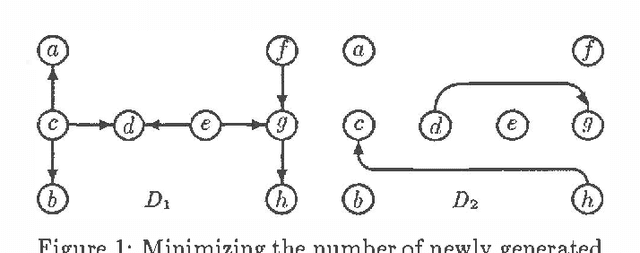
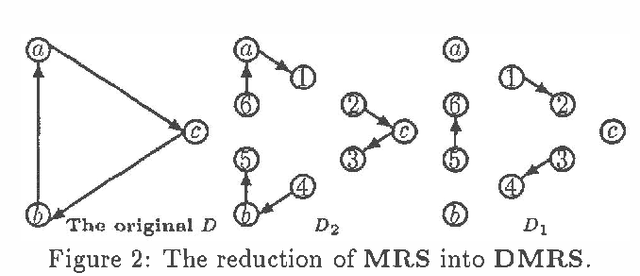
One topic that is likely to attract an increasing amount of attention within the Knowledge-base systems research community is the coordination of information provided by multiple experts. We envision a situation in which several experts independently encode information as belief networks. A potential user must then coordinate the conclusions and recommendations of these networks to derive some sort of consensus. One approach to such a consensus is the fusion of the contributed networks into a single, consensus model prior to the consideration of any case-specific data (specific observations, test results). This approach requires two types of combination procedures, one for probabilities, and one for graphs. Since the combination of probabilities is relatively well understood, the key barriers to this approach lie in the realm of graph theory. This paper provides formal definitions of some of the operations necessary to effect the necessary graphical combinations, and provides complexity analyses of these procedures. The paper's key result is that most of these operations are NP-hard, and its primary message is that the derivation of ?good? consensus networks must be done heuristically.