Deriving a Minimal I-map of a Belief Network Relative to a Target Ordering of its Nodes

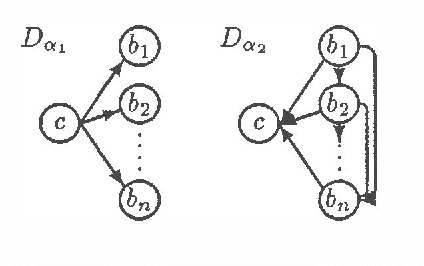
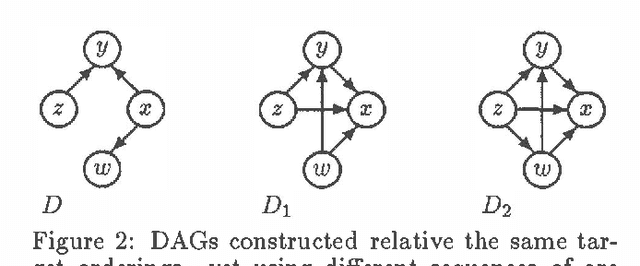
This paper identifies and solves a new optimization problem: Given a belief network (BN) and a target ordering on its variables, how can we efficiently derive its minimal I-map whose arcs are consistent with the target ordering? We present three solutions to this problem, all of which lead to directed acyclic graphs based on the original BN's recursive basis relative to the specified ordering (such a DAG is sometimes termed the boundary DAG drawn from the given BN relative to the said ordering [5]). Along the way, we also uncover an important general principal about arc reversals: when reordering a BN according to some target ordering, (while attempting to minimize the number of arcs generated), the sequence of arc reversals should follow the topological ordering induced by the original belief network's arcs to as great an extent as possible. These results promise to have a significant impact on the derivation of consensus models, as well as on other algorithms that require the reconfiguration and/or combination of BN's.