Ittai Abraham
How Many Workers to Ask? Adaptive Exploration for Collecting High Quality Labels
May 19, 2016
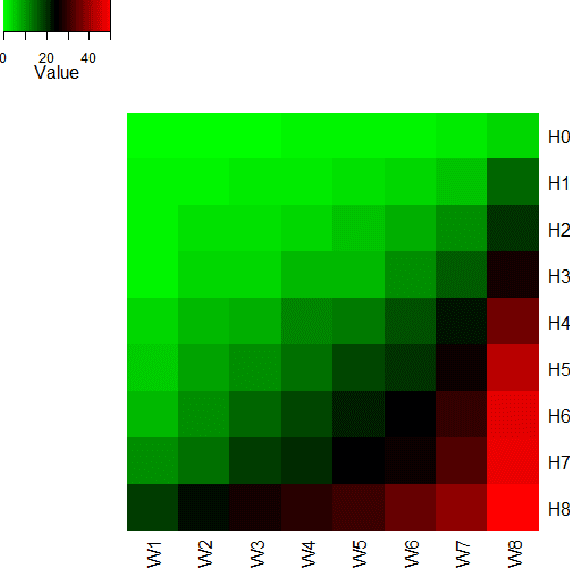
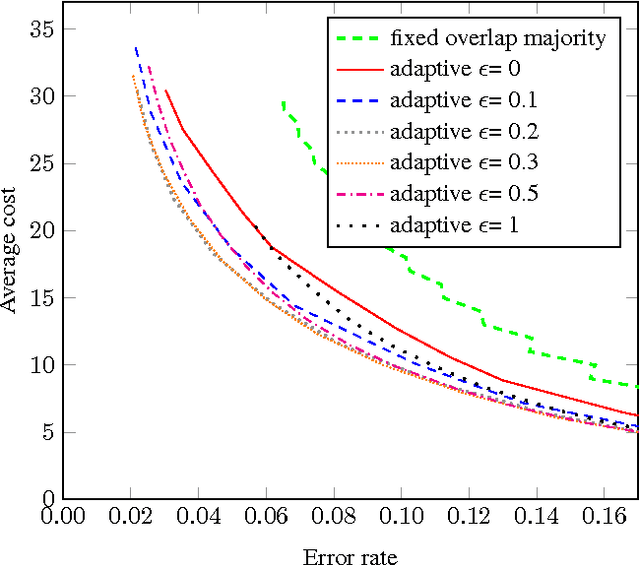
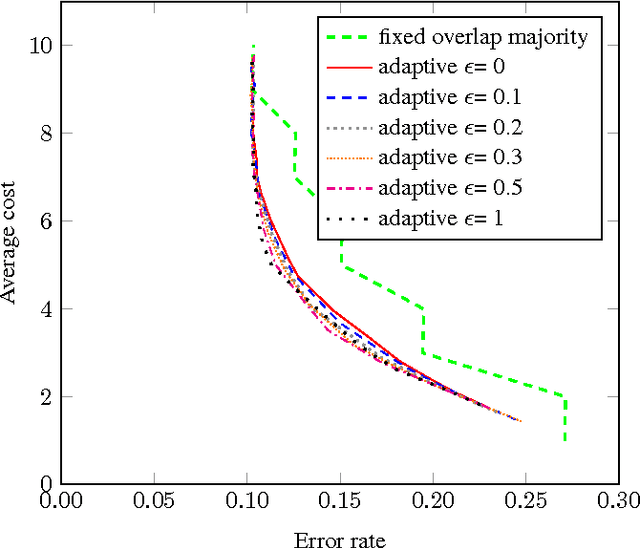
Abstract:Crowdsourcing has been part of the IR toolbox as a cheap and fast mechanism to obtain labels for system development and evaluation. Successful deployment of crowdsourcing at scale involves adjusting many variables, a very important one being the number of workers needed per human intelligence task (HIT). We consider the crowdsourcing task of learning the answer to simple multiple-choice HITs, which are representative of many relevance experiments. In order to provide statistically significant results, one often needs to ask multiple workers to answer the same HIT. A stopping rule is an algorithm that, given a HIT, decides for any given set of worker answers if the system should stop and output an answer or iterate and ask one more worker. Knowing the historic performance of a worker in the form of a quality score can be beneficial in such a scenario. In this paper we investigate how to devise better stopping rules given such quality scores. We also suggest adaptive exploration as a promising approach for scalable and automatic creation of ground truth. We conduct a data analysis on an industrial crowdsourcing platform, and use the observations from this analysis to design new stopping rules that use the workers' quality scores in a non-trivial manner. We then perform a simulation based on a real-world workload, showing that our algorithm performs better than the more naive approaches.
Adaptive Crowdsourcing Algorithms for the Bandit Survey Problem
May 20, 2013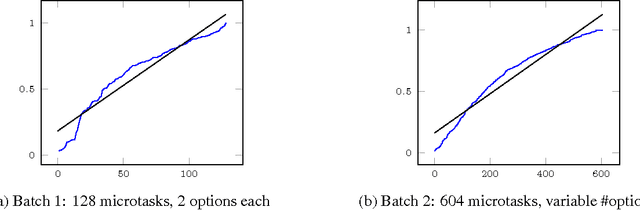
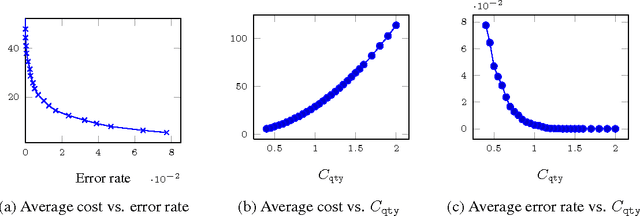
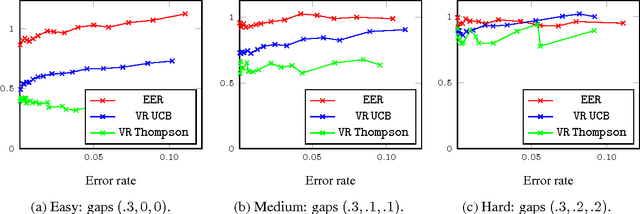
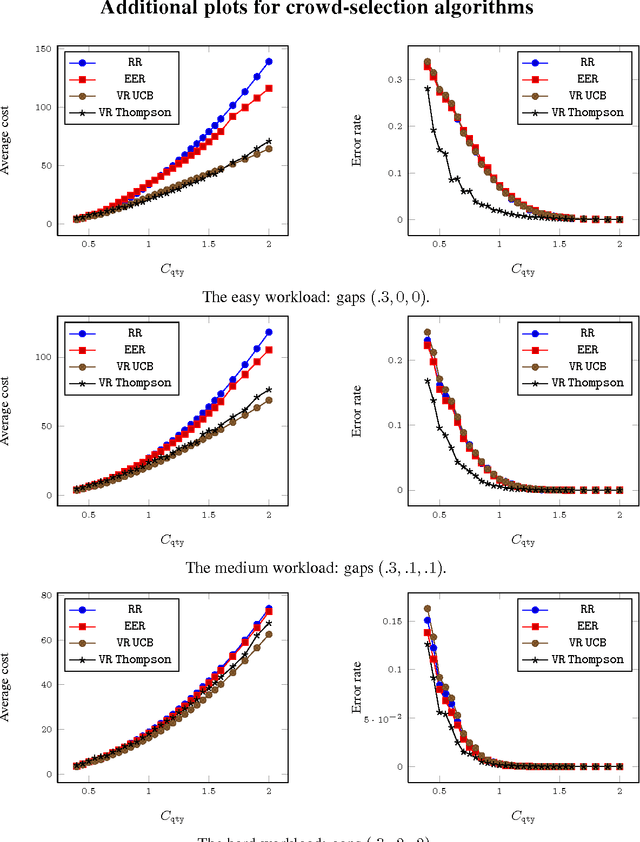
Abstract:Very recently crowdsourcing has become the de facto platform for distributing and collecting human computation for a wide range of tasks and applications such as information retrieval, natural language processing and machine learning. Current crowdsourcing platforms have some limitations in the area of quality control. Most of the effort to ensure good quality has to be done by the experimenter who has to manage the number of workers needed to reach good results. We propose a simple model for adaptive quality control in crowdsourced multiple-choice tasks which we call the \emph{bandit survey problem}. This model is related to, but technically different from the well-known multi-armed bandit problem. We present several algorithms for this problem, and support them with analysis and simulations. Our approach is based in our experience conducting relevance evaluation for a large commercial search engine.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge