A variational Bayes approach to debiased inference for low-dimensional parameters in high-dimensional linear regression

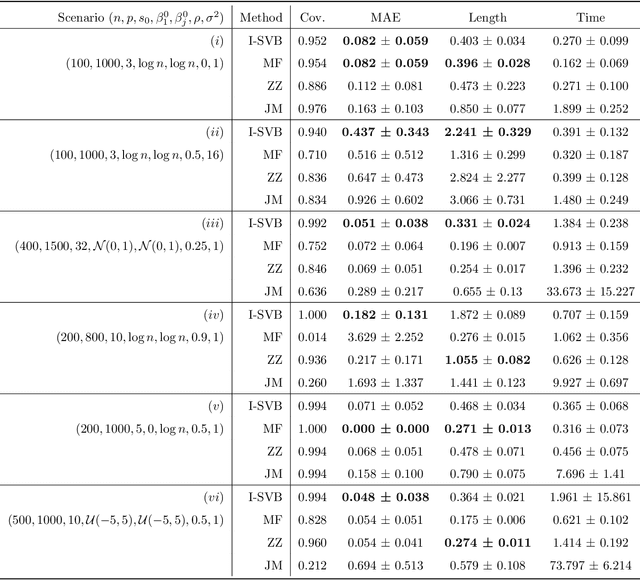
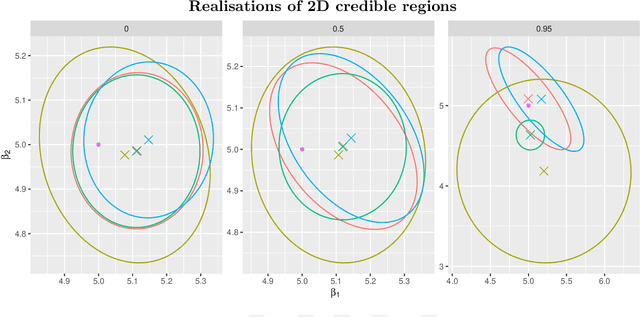
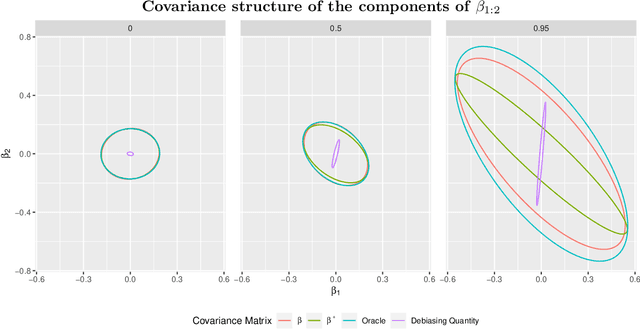
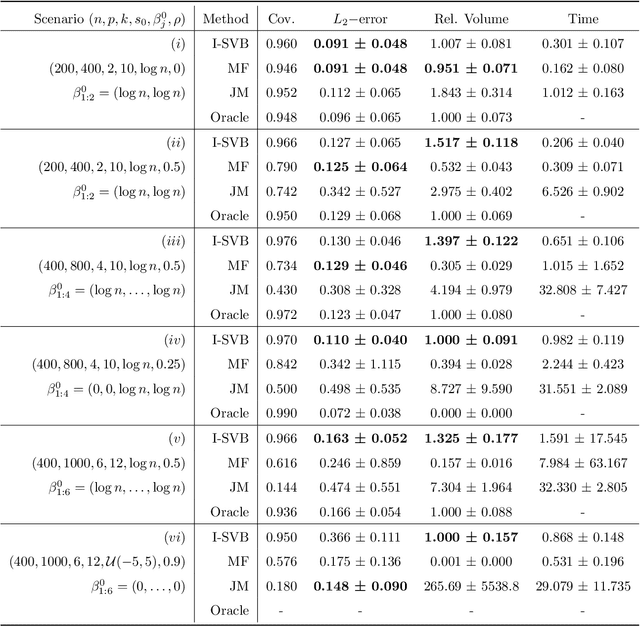
We propose a scalable variational Bayes method for statistical inference for a single or low-dimensional subset of the coordinates of a high-dimensional parameter in sparse linear regression. Our approach relies on assigning a mean-field approximation to the nuisance coordinates and carefully modelling the conditional distribution of the target given the nuisance. This requires only a preprocessing step and preserves the computational advantages of mean-field variational Bayes, while ensuring accurate and reliable inference for the target parameter, including for uncertainty quantification. We investigate the numerical performance of our algorithm, showing that it performs competitively with existing methods. We further establish accompanying theoretical guarantees for estimation and uncertainty quantification in the form of a Bernstein--von Mises theorem.

Posterior and variational inference for deep neural networks with heavy-tailed weights

We consider deep neural networks in a Bayesian framework with a prior distribution sampling the network weights at random. Following a recent idea of Agapiou and Castillo (2023), who show that heavy-tailed prior distributions achieve automatic adaptation to smoothness, we introduce a simple Bayesian deep learning prior based on heavy-tailed weights and ReLU activation. We show that the corresponding posterior distribution achieves near-optimal minimax contraction rates, simultaneously adaptive to both intrinsic dimension and smoothness of the underlying function, in a variety of contexts including nonparametric regression, geometric data and Besov spaces. While most works so far need a form of model selection built-in within the prior distribution, a key aspect of our approach is that it does not require to sample hyperparameters to learn the architecture of the network. We also provide variational Bayes counterparts of the results, that show that mean-field variational approximations still benefit from near-optimal theoretical support.

Deep Horseshoe Gaussian Processes

Deep Gaussian processes have recently been proposed as natural objects to fit, similarly to deep neural networks, possibly complex features present in modern data samples, such as compositional structures. Adopting a Bayesian nonparametric approach, it is natural to use deep Gaussian processes as prior distributions, and use the corresponding posterior distributions for statistical inference. We introduce the deep Horseshoe Gaussian process Deep-HGP, a new simple prior based on deep Gaussian processes with a squared-exponential kernel, that in particular enables data-driven choices of the key lengthscale parameters. For nonparametric regression with random design, we show that the associated tempered posterior distribution recovers the unknown true regression curve optimally in terms of quadratic loss, up to a logarithmic factor, in an adaptive way. The convergence rates are simultaneously adaptive to both the smoothness of the regression function and to its structure in terms of compositions. The dependence of the rates in terms of dimension are explicit, allowing in particular for input spaces of dimension increasing with the number of observations.

Semiparametric inference using fractional posteriors

We establish a general Bernstein--von Mises theorem for approximately linear semiparametric functionals of fractional posterior distributions based on nonparametric priors. This is illustrated in a number of nonparametric settings and for different classes of prior distributions, including Gaussian process priors. We show that fractional posterior credible sets can provide reliable semiparametric uncertainty quantification, but have inflated size. To remedy this, we further propose a \textit{shifted-and-rescaled} fractional posterior set that is an efficient confidence set having optimal size under regularity conditions. As part of our proofs, we also refine existing contraction rate results for fractional posteriors by sharpening the dependence of the rate on the fractional exponent.