Integrating RIS into HAP Networks for Improved Connectivity

This paper investigates a high-altitude platform (HAP) network enhanced with reconfigurable intelligent surfaces (RISs). The arbitrary placement of HAPs and RISs is modeled using stochastic geometry, specifically as homogeneous Poisson point processes. The HAP--RIS links are assumed to follow Rician fading, while the RIS--user links experience shadowed-Rician fading. The system's coverage probability and ergodic capacity are derived analytically and validated through Monte Carlo simulations. The results highlight significant performance gains and demonstrate the influence of various system parameters and fading conditions. The proposed system has potential for enhancing connectivity and data offloading in practical scenarios.

Enhancing HAP Networks with Reconfigurable Intelligent Surfaces

This paper presents and analyzes a reconfigurable intelligent surface (RIS)-based high-altitude platform (HAP) network. Stochastic geometry is used to model the arbitrary locations of the HAPs and RISs as a homogenous Poisson point process. Considering that the links between the HAPs, RISs, and users are $\kappa$--$\mu$ faded, the coverage and ergodic capacity of the proposed system are expressed. The analytically derived performance measures are verified through Monte Carlo simulations. Significant improvements in system performance and the impact of system parameters are demonstrated in the results. Thus, the proposed system concept can improve connectivity and data offloading in smart cities and dense urban environments.

3D Reconfigurable Intelligent Surfaces for Satellite-Terrestrial Networks

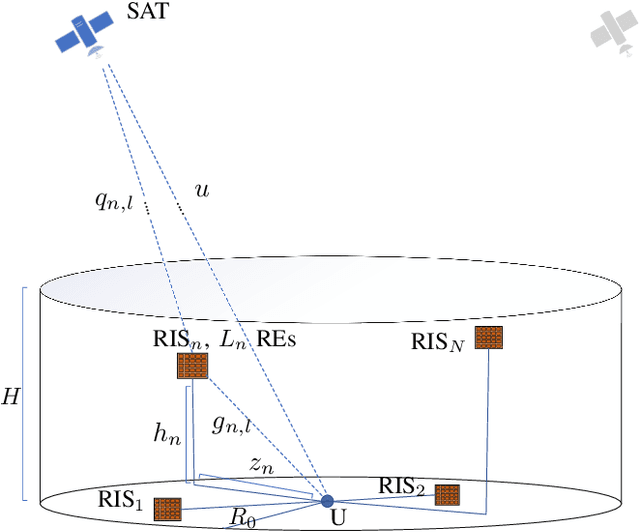
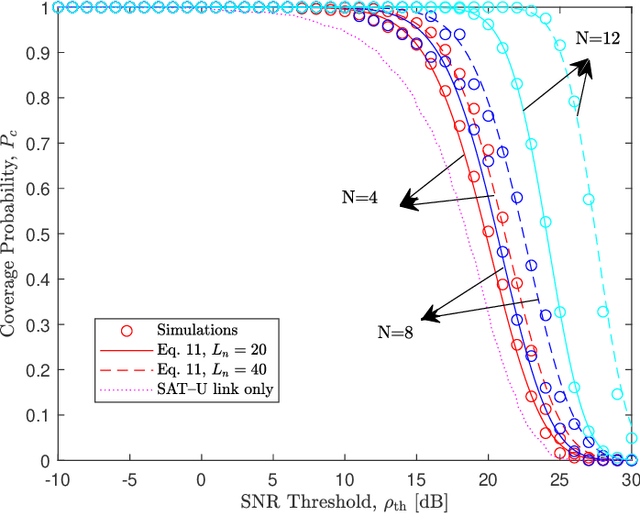
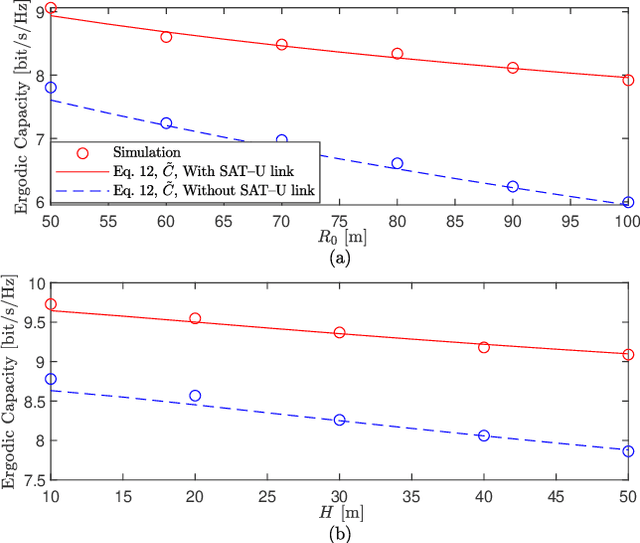
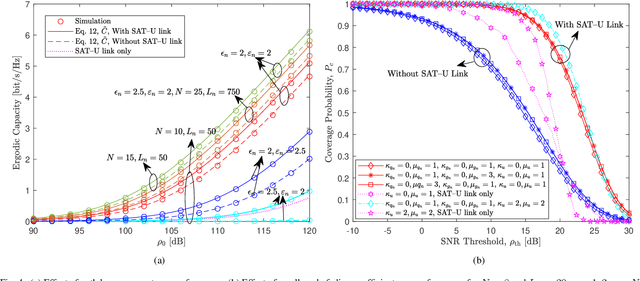
This paper proposes a three-dimensional (3D) satellite-terrestrial communication network assisted with reconfigurable intelligent surfaces (RISs). Using stochastic geometry models, we present an original framework to derive tractable yet accurate closed-form expressions for coverage probability and ergodic capacity in the presence of fading. A homogeneous Poisson point process models the satellites on a sphere, while RISs are randomly deployed in a 3D cylindrical region. We consider nonidentical channels that correspond to different RISs and follow the {\kappa}-{\mu} fading distribution. We verify the high accuracy of the adopted approach through Monte Carlo simulations and demonstrate the significant improvement in system performance due to using RISs. Furthermore, we comprehensively study the effect of the different system parameters on its performance using the derived analytical expressions, which enable system engineers to predict and optimize the expected downlink coverage and capacity performance analytically.

Improved Coefficients for the Karagiannidis-Lioumpas Approximations and Bounds to the Gaussian Q-Function

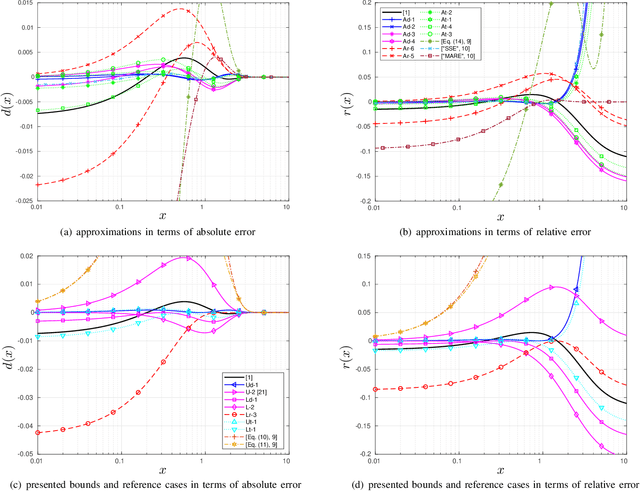
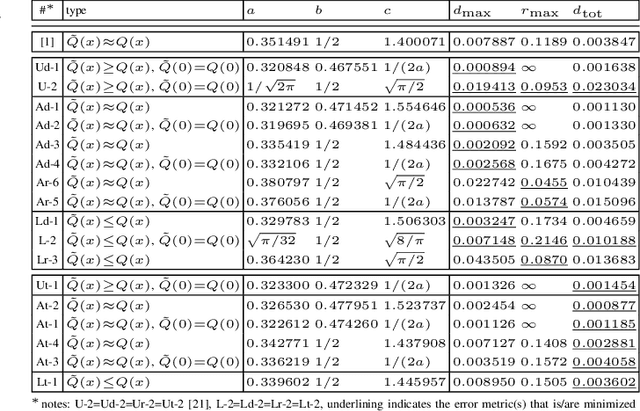
We revisit the Karagiannidis-Lioumpas (KL) approximation of the Q-function by optimizing its coefficients in terms of absolute error, relative error and total error. For minimizing the maximum absolute/relative error, we describe the targeted uniform error functions by sets of nonlinear equations so that the optimized coefficients are the solutions thereof. The total error is minimized with numerical search. We also introduce an extra coefficient in the KL approximation to achieve significantly tighter absolute and total error at the expense of unbounded relative error. Furthermore, we extend the KL expression to lower and upper bounds with optimized coefficients that minimize the error measures in the same way as for the approximations.