Improved Coefficients for the Karagiannidis-Lioumpas Approximations and Bounds to the Gaussian Q-Function
Paper and Code
Jan 19, 2021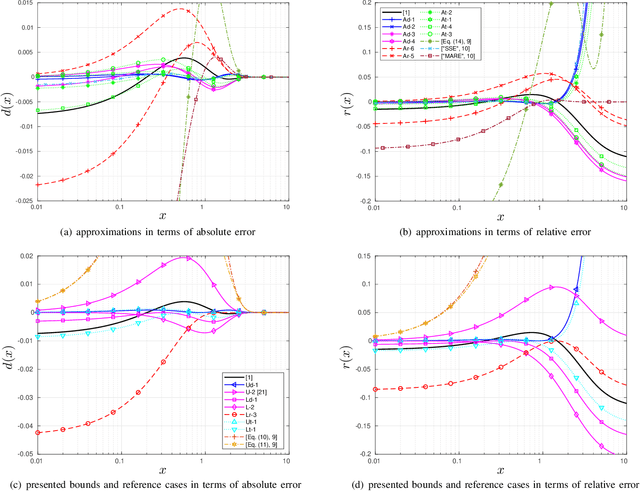
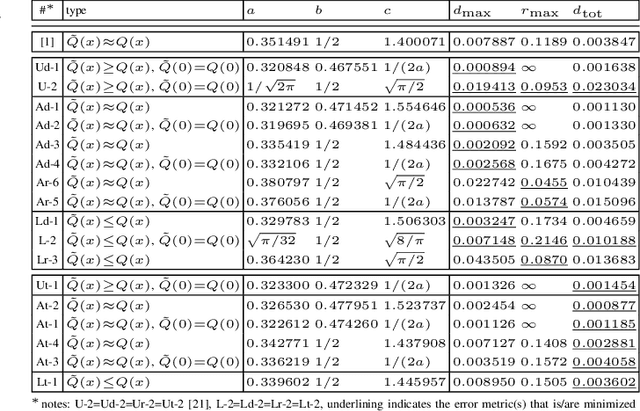
We revisit the Karagiannidis-Lioumpas (KL) approximation of the Q-function by optimizing its coefficients in terms of absolute error, relative error and total error. For minimizing the maximum absolute/relative error, we describe the targeted uniform error functions by sets of nonlinear equations so that the optimized coefficients are the solutions thereof. The total error is minimized with numerical search. We also introduce an extra coefficient in the KL approximation to achieve significantly tighter absolute and total error at the expense of unbounded relative error. Furthermore, we extend the KL expression to lower and upper bounds with optimized coefficients that minimize the error measures in the same way as for the approximations.
* IEEE Communications Letters
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge