BigBraveBN: algorithm of structural learning for bayesian networks with a large number of nodes

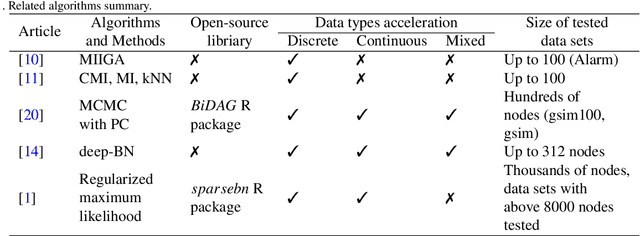
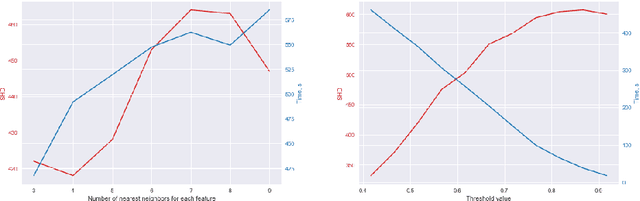
Learning a Bayesian network is an NP-hard problem and with an increase in the number of nodes, classical algorithms for learning the structure of Bayesian networks become inefficient. In recent years, some methods and algorithms for learning Bayesian networks with a high number of nodes (more than 50) were developed. But these solutions have their disadvantages, for instance, they only operate one type of data (discrete or continuous) or their algorithm has been created to meet a specific nature of data (medical, social, etc.). The article presents a BigBraveBN algorithm for learning large Bayesian Networks with a high number of nodes (over 100). The algorithm utilizes the Brave coefficient that measures the mutual occurrence of instances in several groups. To form these groups, we use the method of nearest neighbours based on the Mutual information (MI) measure. In the experimental part of the article, we compare the performance of BigBraveBN to other existing solutions on multiple data sets both discrete and continuous. The experimental part also represents tests on real data. The aforementioned experimental results demonstrate the efficiency of the BigBraveBN algorithm in structure learning of Bayesian Networks.

Oil reservoir recovery factor assessment using Bayesian networks based on advanced approaches to analogues clustering

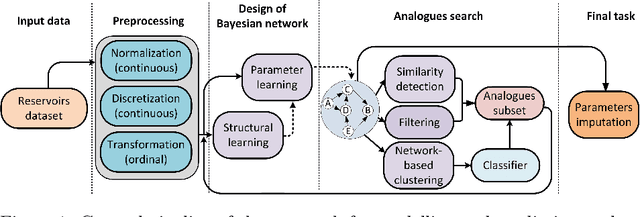
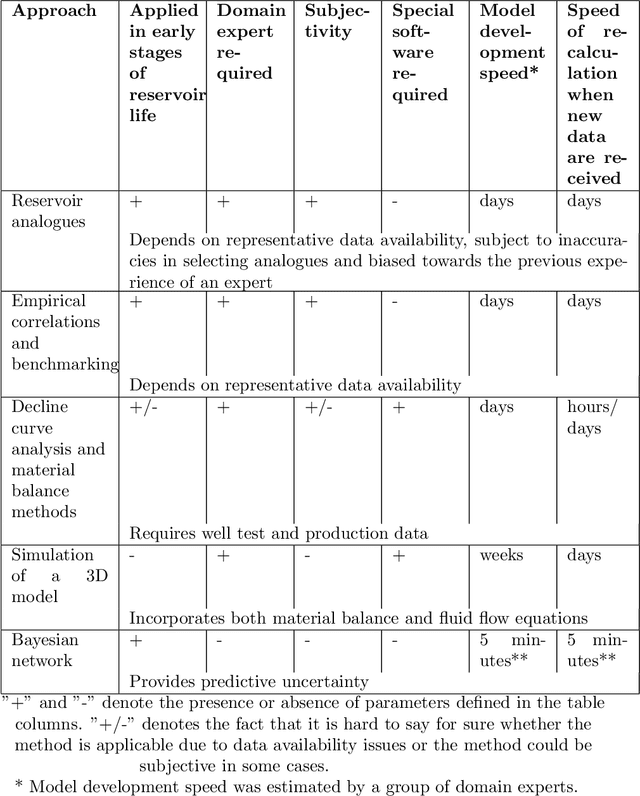
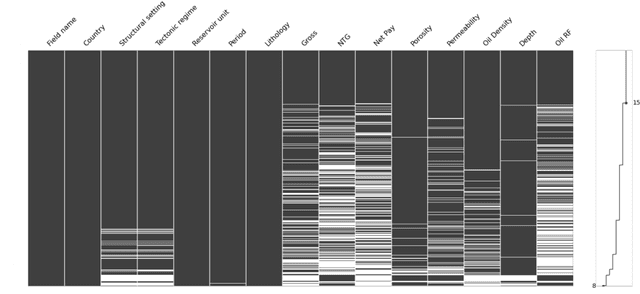
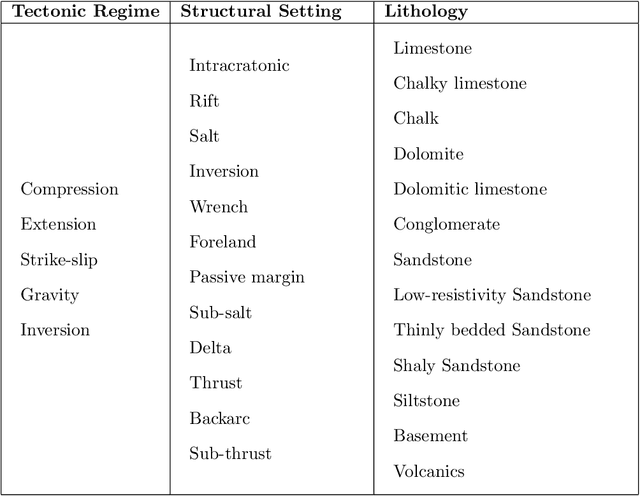
The work focuses on the modelling and imputation of oil and gas reservoirs parameters, specifically, the problem of predicting the oil recovery factor (RF) using Bayesian networks (BNs). Recovery forecasting is critical for the oil and gas industry as it directly affects a company's profit. However, current approaches to forecasting the RF are complex and computationally expensive. In addition, they require vast amount of data and are difficult to constrain in the early stages of reservoir development. To address this problem, we propose a BN approach and describe ways to improve parameter predictions' accuracy. Various training hyperparameters for BNs were considered, and the best ones were used. The approaches of structure and parameter learning, data discretization and normalization, subsampling on analogues of the target reservoir, clustering of networks and data filtering were considered. Finally, a physical model of a synthetic oil reservoir was used to validate BNs' predictions of the RF. All approaches to modelling based on BNs provide full coverage of the confidence interval for the RF predicted by the physical model, but at the same time require less time and data for modelling, which demonstrates the possibility of using in the early stages of reservoirs development. The main result of the work can be considered the development of a methodology for studying the parameters of reservoirs based on Bayesian networks built on small amounts of data and with minimal involvement of expert knowledge. The methodology was tested on the example of the problem of the recovery factor imputation.

MIxBN: library for learning Bayesian networks from mixed data

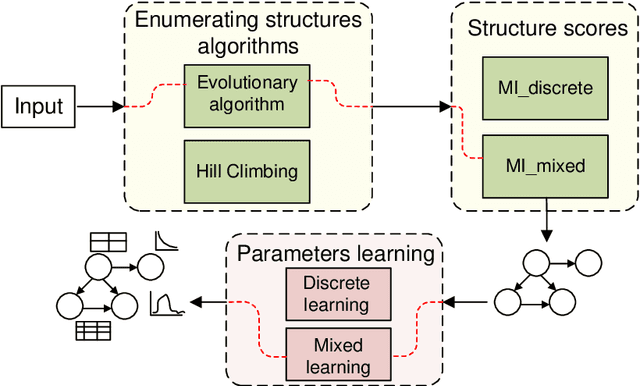
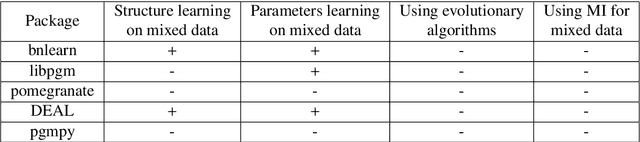
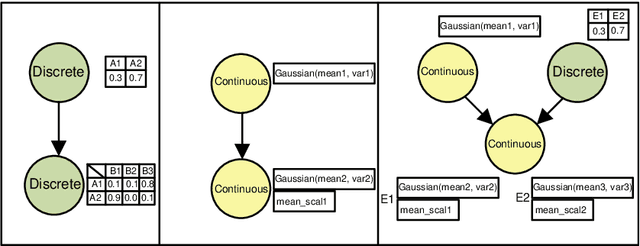
This paper describes a new library for learning Bayesian networks from data containing discrete and continuous variables (mixed data). In addition to the classical learning methods on discretized data, this library proposes its algorithm that allows structural learning and parameters learning from mixed data without discretization since data discretization leads to information loss. This algorithm based on mixed MI score function for structural learning, and also linear regression and Gaussian distribution approximation for parameters learning. The library also offers two algorithms for enumerating graph structures - the greedy Hill-Climbing algorithm and the evolutionary algorithm. Thus the key capabilities of the proposed library are as follows: (1) structural and parameters learning of a Bayesian network on discretized data, (2) structural and parameters learning of a Bayesian network on mixed data using the MI mixed score function and Gaussian approximation, (3) launching learning algorithms on one of two algorithms for enumerating graph structures - Hill-Climbing and the evolutionary algorithm. Since the need for mixed data representation comes from practical necessity, the advantages of our implementations are evaluated in the context of solving approximation and gap recovery problems on synthetic data and real datasets.

Oil and Gas Reservoirs Parameters Analysis Using Mixed Learning of Bayesian Networks

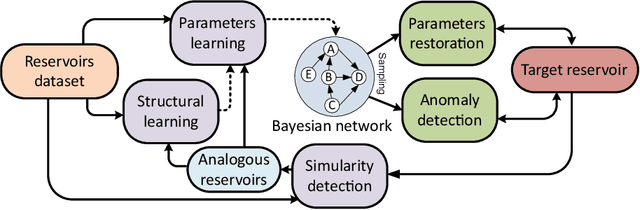
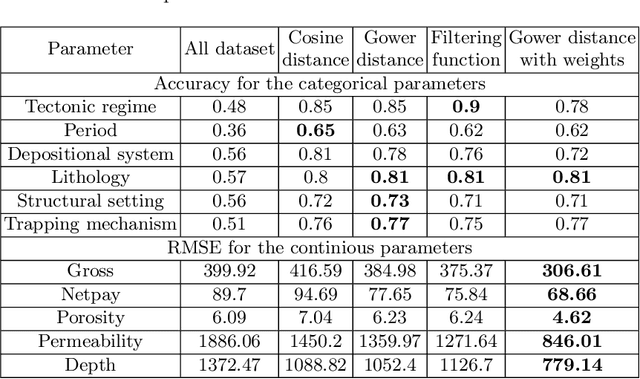
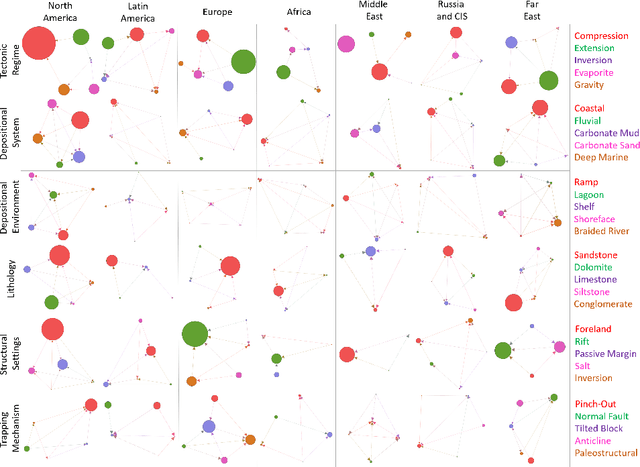
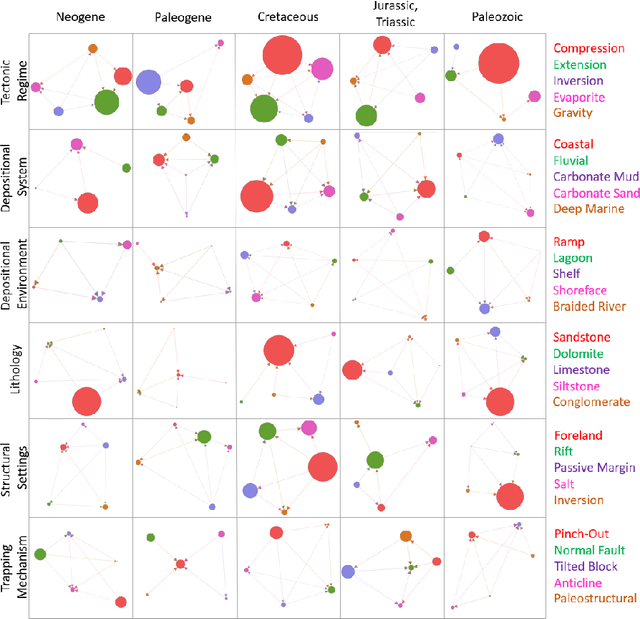
In this paper, a multipurpose Bayesian-based method for data analysis, causal inference and prediction in the sphere of oil and gas reservoir development is considered. This allows analysing parameters of a reservoir, discovery dependencies among parameters (including cause and effects relations), checking for anomalies, prediction of expected values of missing parameters, looking for the closest analogues, and much more. The method is based on extended algorithm MixLearn@BN for structural learning of Bayesian networks. Key ideas of MixLearn@BN are following: (1) learning the network structure on homogeneous data subsets, (2) assigning a part of the structure by an expert, and (3) learning the distribution parameters on mixed data (discrete and continuous). Homogeneous data subsets are identified as various groups of reservoirs with similar features (analogues), where similarity measure may be based on several types of distances. The aim of the described technique of Bayesian network learning is to improve the quality of predictions and causal inference on such networks. Experimental studies prove that the suggested method gives a significant advantage in missing values prediction and anomalies detection accuracy. Moreover, the method was applied to the database of more than a thousand petroleum reservoirs across the globe and allowed to discover novel insights in geological parameters relationships.