Approach of variable clustering and compression for learning large Bayesian networks

This paper describes a new approach for learning structures of large Bayesian networks based on blocks resulting from feature space clustering. This clustering is obtained using normalized mutual information. And the subsequent aggregation of blocks is done using classical learning methods except that they are input with compressed information about combinations of feature values for each block. Validation of this approach is done for Hill-Climbing as a graph enumeration algorithm for two score functions: BIC and MI. In this way, potentially parallelizable block learning can be implemented even for those score functions that are considered unsuitable for parallelizable learning. The advantage of the approach is evaluated in terms of speed of work as well as the accuracy of the found structures.

MIxBN: library for learning Bayesian networks from mixed data

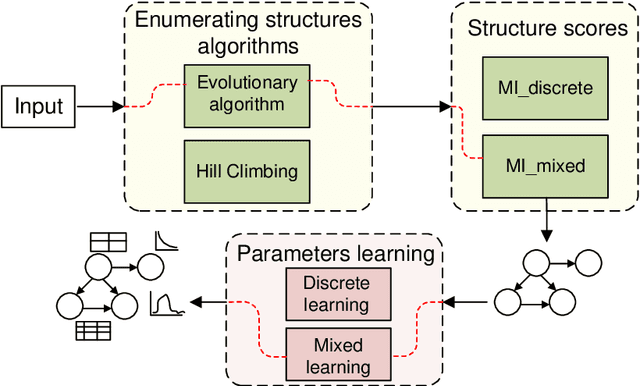
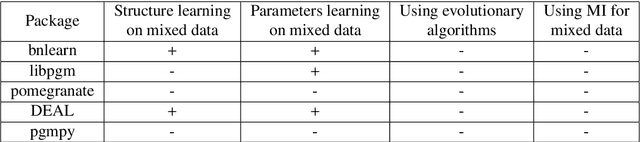
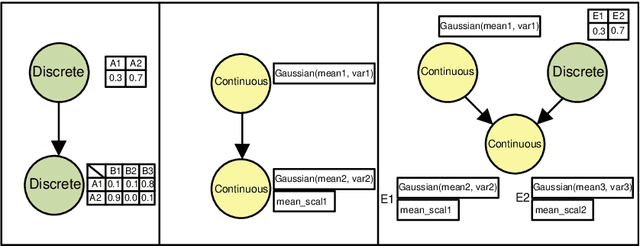
This paper describes a new library for learning Bayesian networks from data containing discrete and continuous variables (mixed data). In addition to the classical learning methods on discretized data, this library proposes its algorithm that allows structural learning and parameters learning from mixed data without discretization since data discretization leads to information loss. This algorithm based on mixed MI score function for structural learning, and also linear regression and Gaussian distribution approximation for parameters learning. The library also offers two algorithms for enumerating graph structures - the greedy Hill-Climbing algorithm and the evolutionary algorithm. Thus the key capabilities of the proposed library are as follows: (1) structural and parameters learning of a Bayesian network on discretized data, (2) structural and parameters learning of a Bayesian network on mixed data using the MI mixed score function and Gaussian approximation, (3) launching learning algorithms on one of two algorithms for enumerating graph structures - Hill-Climbing and the evolutionary algorithm. Since the need for mixed data representation comes from practical necessity, the advantages of our implementations are evaluated in the context of solving approximation and gap recovery problems on synthetic data and real datasets.