An Inherent Trade-Off in Noisy Neural Communication with Rank-Order Coding

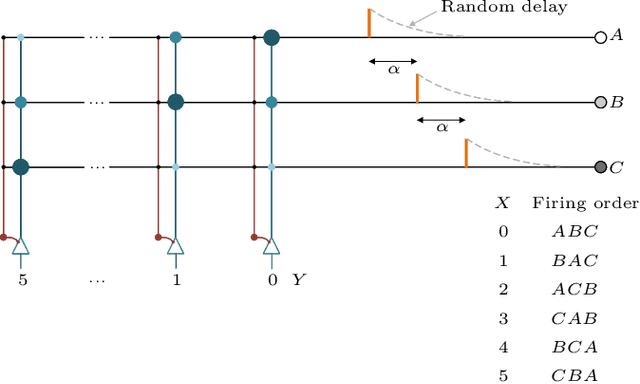
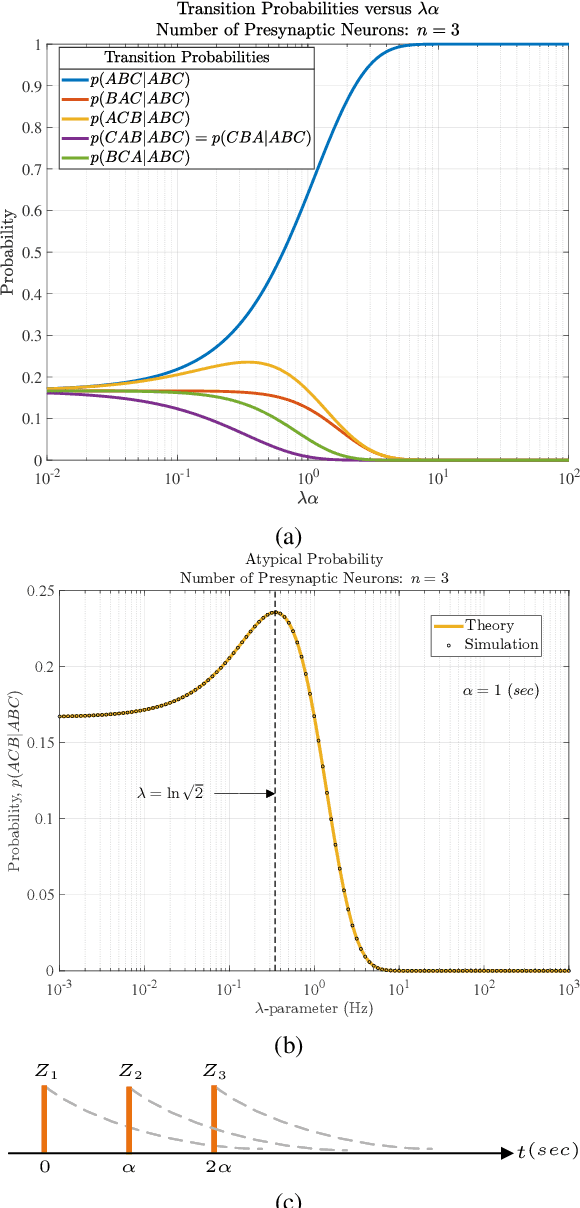
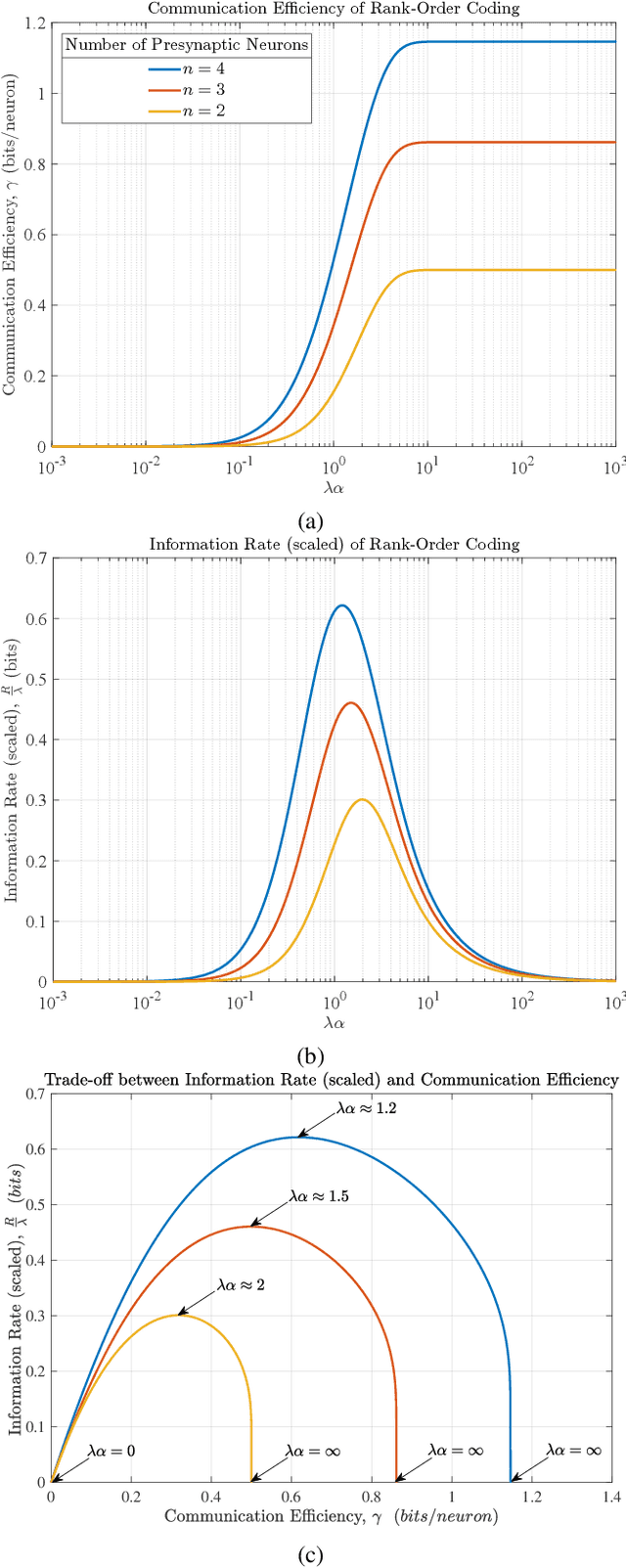
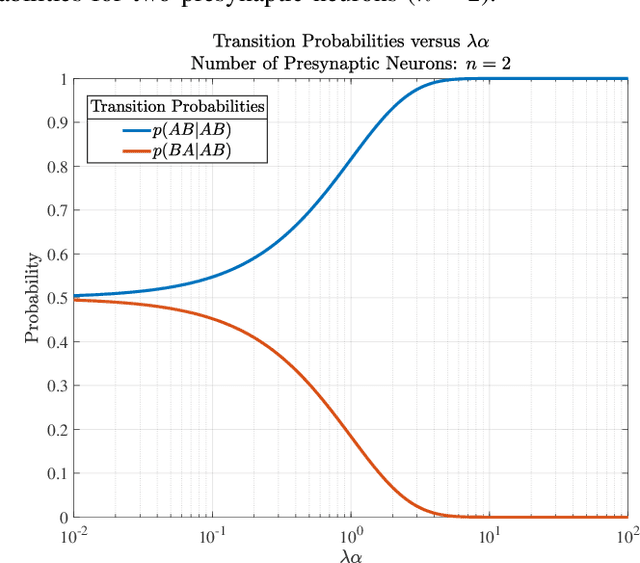
Rank-order coding, a form of temporal coding, has emerged as a promising scheme to explain the rapid ability of the mammalian brain. Owing to its speed as well as efficiency, rank-order coding is increasingly gaining interest in diverse research areas beyond neuroscience. However, much uncertainty still exists about the performance of rank-order coding under noise. Herein we show what information rates are fundamentally possible and what trade-offs are at stake. An unexpected finding in this paper is the emergence of a special class of errors that, in a regime, increase with less noise.

An Extension of Fisher's Criterion: Theoretical Results with a Neural Network Realization

Fisher's criterion is a widely used tool in machine learning for feature selection. For large search spaces, Fisher's criterion can provide a scalable solution to select features. A challenging limitation of Fisher's criterion, however, is that it performs poorly when mean values of class-conditional distributions are close to each other. Motivated by this challenge, we propose an extension of Fisher's criterion to overcome this limitation. The proposed extension utilizes the available heteroscedasticity of class-conditional distributions to distinguish one class from another. Additionally, we describe how our theoretical results can be casted into a neural network framework, and conduct a proof-of-concept experiment to demonstrate the viability of our approach to solve classification problems.

Imaging with SPADs and DMDs: Seeing through Diffraction-Photons

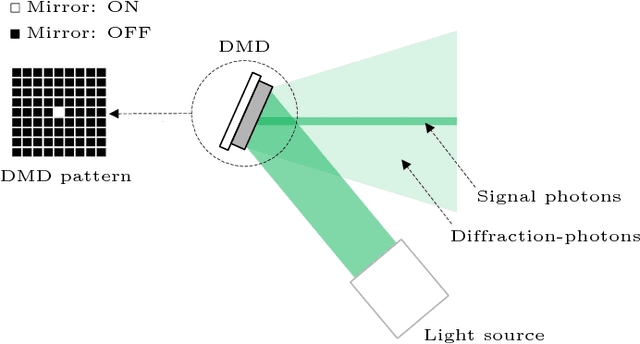
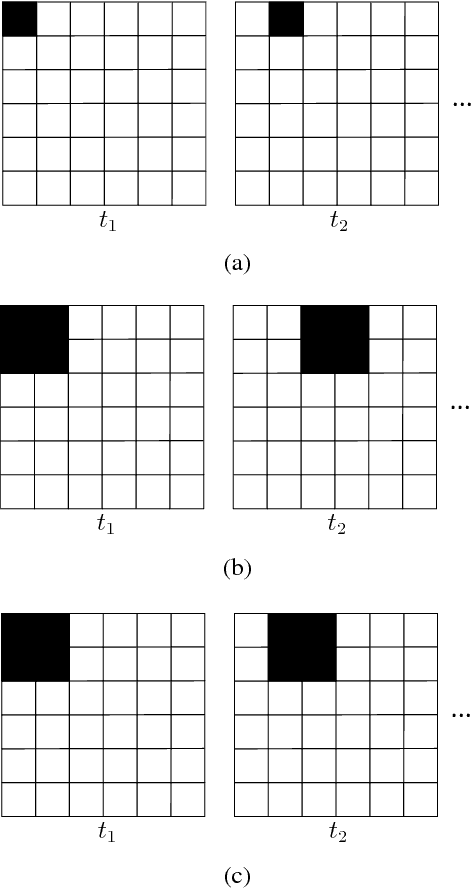
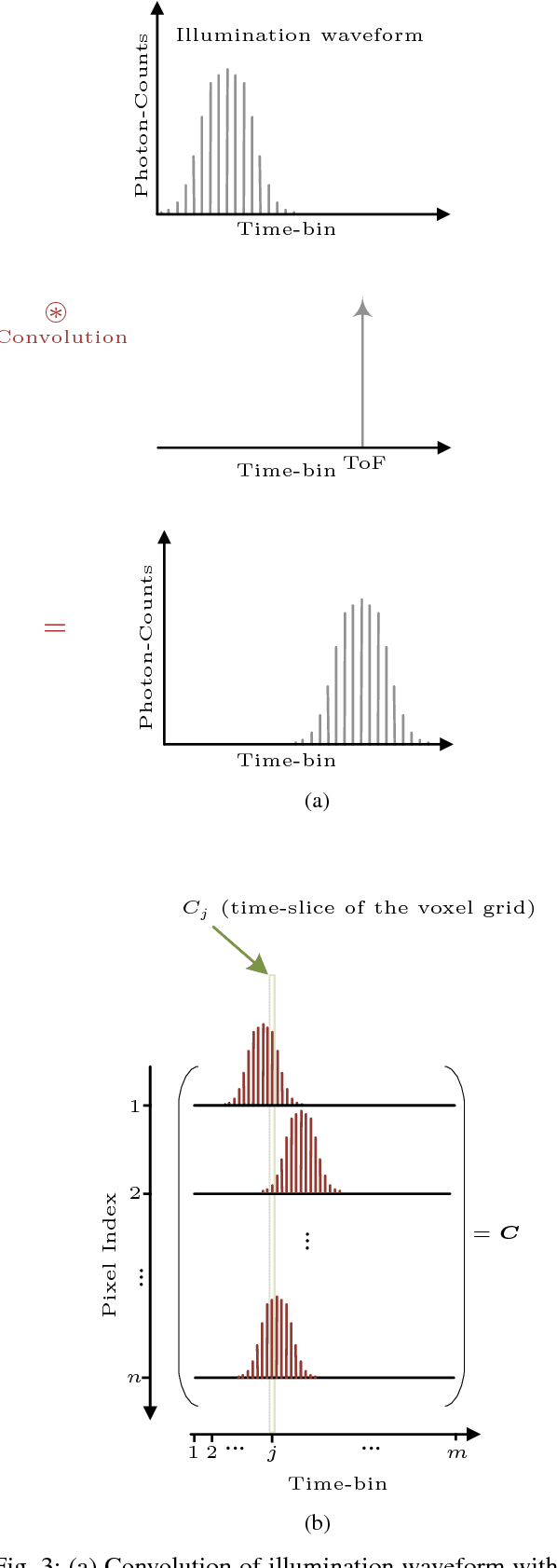
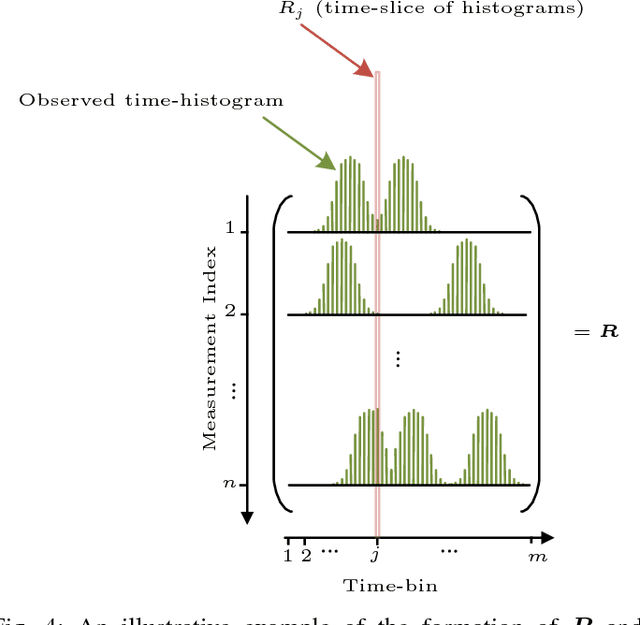
This paper addresses the problem of imaging in the presence of diffraction-photons. Diffraction-photons arise from the low contrast-ratio of DMDs ($\sim 1000: 1$), and very much degrade the quality of images captured by SPAD-based systems. Herein, a joint illumination/deconvolution scheme is designed to overcome diffraction-photons, enabling the acquisition of intensity and depth images. Additionally, a proof-of-concept experiment is conducted to demonstrate the viability of the designed scheme. It is shown that by co-designing the illumination and deconvolution phases of imaging, one can substantially overcome diffraction-photons.