Huiping Duan
Near/Far-Field Channel Estimation For Terahertz Systems With ELAAs: A Block-Sparse-Aware Approach
Apr 08, 2024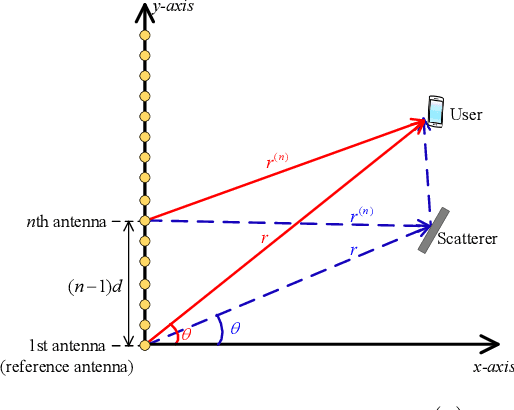



Abstract:Millimeter wave/Terahertz (mmWave/THz) communication with extremely large-scale antenna arrays (ELAAs) offers a promising solution to meet the escalating demand for high data rates in next-generation communications. A large array aperture, along with the ever increasing carrier frequency within the mmWave/THz bands, leads to a large Rayleigh distance. As a result, the traditional plane-wave assumption may not hold valid for mmWave/THz systems featuring ELAAs. In this paper, we consider the problem of hybrid near/far-field channel estimation by taking spherical wave propagation into account. By analyzing the coherence properties of any two near-field steering vectors, we prove that the hybrid near/far-field channel admits a block-sparse representation on a specially designed orthogonal dictionary. Specifically, the percentage of nonzero elements of such a block-sparse representation decreases in the order of $1/\sqrt{N}$, which tends to zero as the number of antennas, $N$, grows. Such a block-sparse representation allows to convert channel estimation into a block-sparse signal recovery problem. Simulation results are provided to verify our theoretical results and illustrate the performance of the proposed channel estimation approach in comparison with existing state-of-the-art methods.
Spatial Channel Covariance Estimation and Two-Timescale Beamforming for IRS-Assisted Millimeter Wave Systems
Apr 17, 2022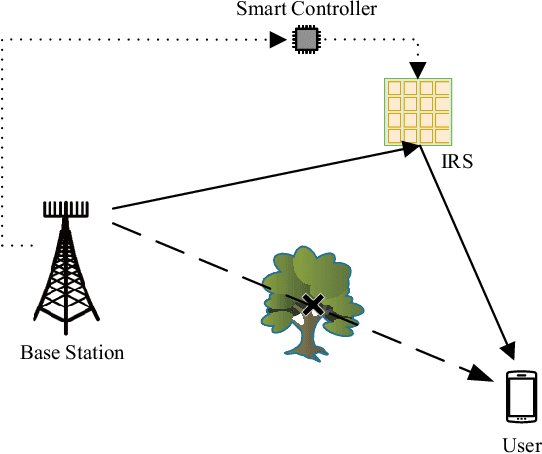
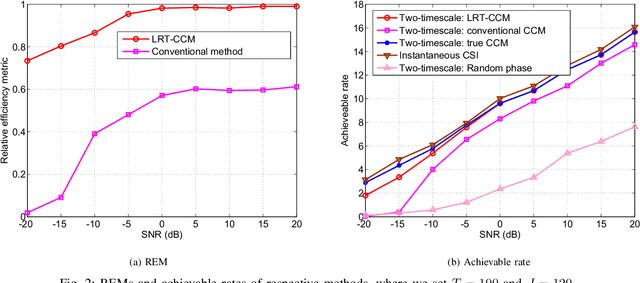
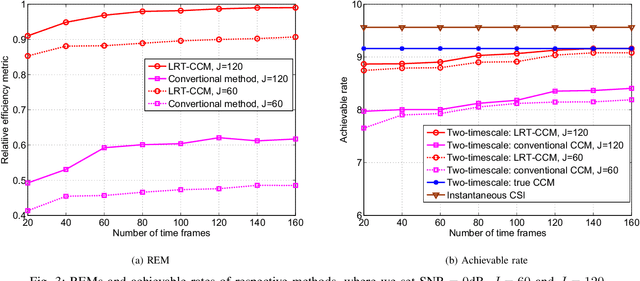
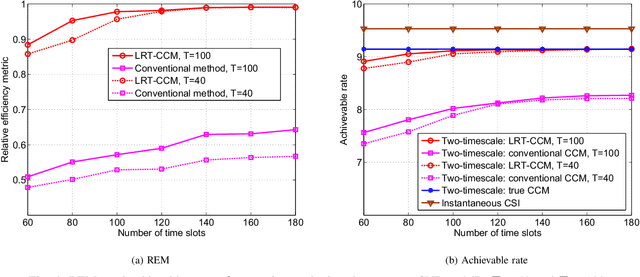
Abstract:We consider the problem of spatial channel covariance matrix (CCM) estimation for intelligent reflecting surface (IRS)-assisted millimeter wave (mmWave) communication systems. Spatial CCM is essential for two-timescale beamforming in IRS-assisted systems; however, estimating the spatial CCM is challenging due to the passive nature of reflecting elements and the large size of the CCM resulting from massive reflecting elements of the IRS. In this paper, we propose a CCM estimation method by exploiting the low-rankness as well as the positive semi-definite (PSD) 3-level Toeplitz structure of the CCM. Estimation of the CCM is formulated as a semidefinite programming (SDP) problem and an alternating direction method of multipliers (ADMM) algorithm is developed. Our analysis shows that the proposed method is theoretically guaranteed to attain a reliable CCM estimate with a sample complexity much smaller than the dimension of the CCM. Thus the proposed method can help achieve a significant training overhead reduction. Simulation results are presented to illustrate the effectiveness of our proposed method and the performance of two-timescale beamforming scheme based on the estimated CCM.
A Variational Bayesian Inference-Inspired Unrolled Deep Network for MIMO Detection
Sep 25, 2021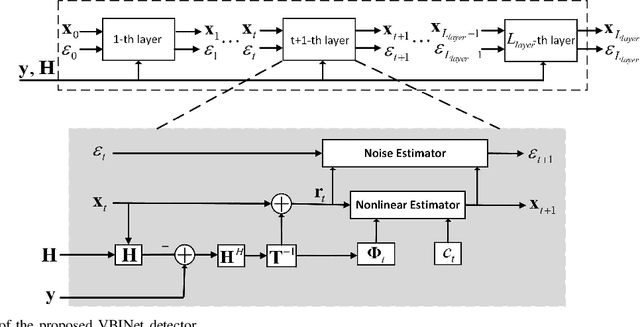

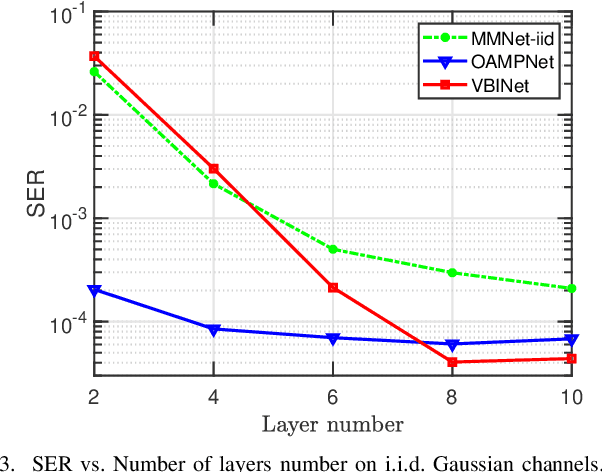
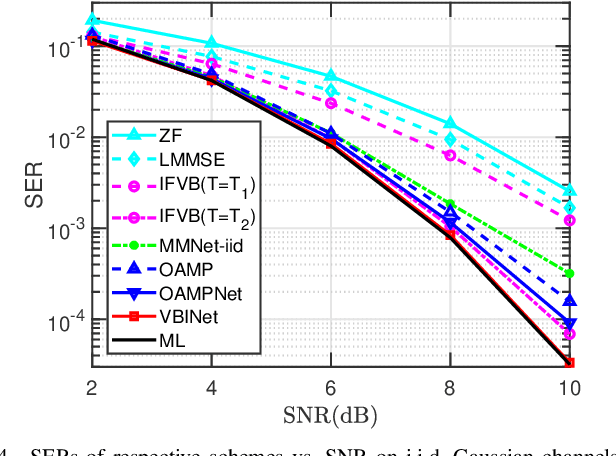
Abstract:The great success of deep learning (DL) has inspired researchers to develop more accurate and efficient symbol detectors for multi-input multi-output (MIMO) systems. Existing DL-based MIMO detectors, however, suffer several drawbacks. To address these issues, in this paper, we develop a modeldriven DL detector based on variational Bayesian inference. Specifically, the proposed unrolled DL architecture is inspired by an inverse-free variational Bayesian learning framework which circumvents matrix inversion via maximizing a relaxed evidence lower bound. Two networks are respectively developed for independent and identically distributed (i.i.d.) Gaussian channels and arbitrarily correlated channels. The proposed networks, referred to as VBINet, have only a few learnable parameters and thus can be efficiently trained with a moderate amount of training samples. The proposed VBINet-based detectors can work in both offline and online training modes. An important advantage of our proposed networks over state-of-the-art MIMO detection networks such as OAMPNet and MMNet is that the VBINet can automatically learn the noise variance from data, thus yielding a significant performance improvement over the OAMPNet and MMNet in the presence of noise variance uncertainty. Simulation results show that the proposed VBINet-based detectors achieve competitive performance for both i.i.d. Gaussian and realistic 3GPP MIMO channels.
Fast Low-Rank Bayesian Matrix Completion with Hierarchical Gaussian Prior Models
Aug 26, 2017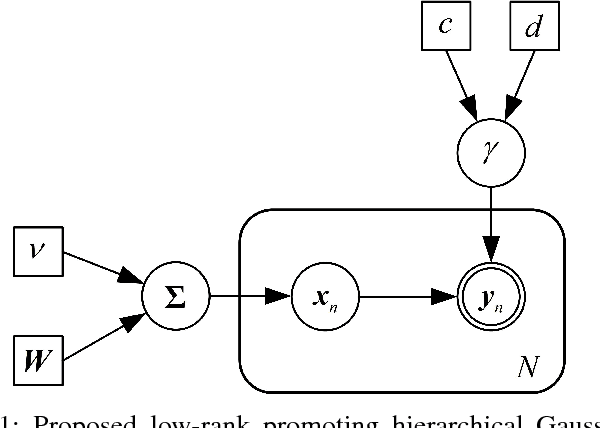
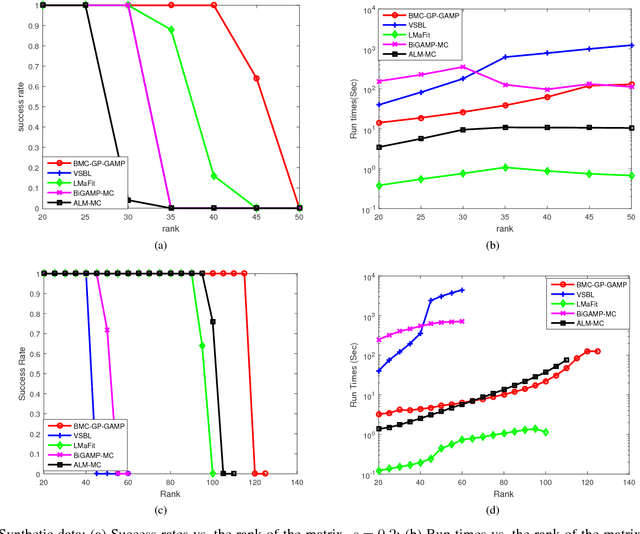


Abstract:The problem of low rank matrix completion is considered in this paper. To exploit the underlying low-rank structure of the data matrix, we propose a hierarchical Gaussian prior model, where columns of the low-rank matrix are assumed to follow a Gaussian distribution with zero mean and a common precision matrix, and a Wishart distribution is specified as a hyperprior over the precision matrix. We show that such a hierarchical Gaussian prior has the potential to encourage a low-rank solution. Based on the proposed hierarchical prior model, a variational Bayesian method is developed for matrix completion, where the generalized approximate massage passing (GAMP) technique is embedded into the variational Bayesian inference in order to circumvent cumbersome matrix inverse operations. Simulation results show that our proposed method demonstrates superiority over existing state-of-the-art matrix completion methods.
Robust Bayesian Compressed sensing
Oct 21, 2016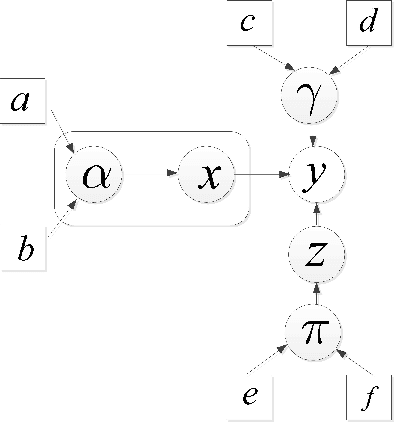
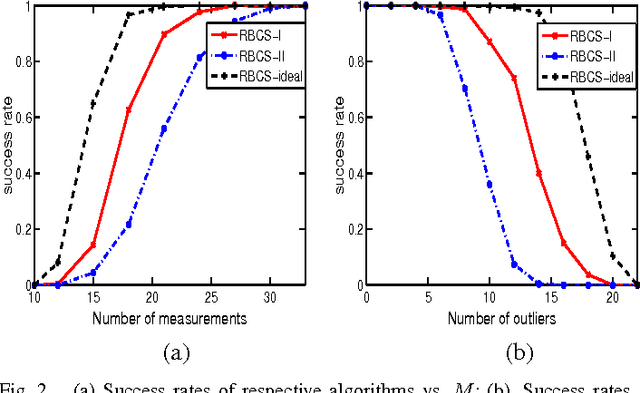
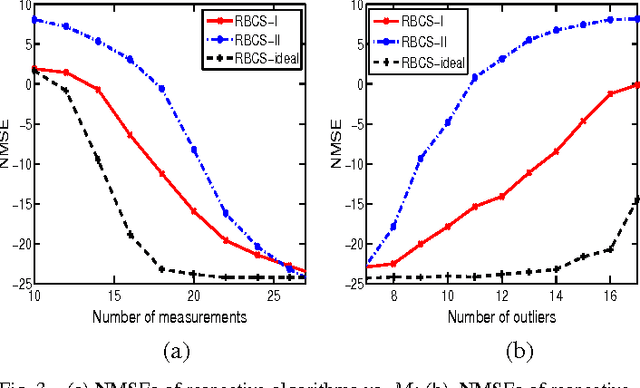
Abstract:We consider the problem of robust compressed sensing whose objective is to recover a high-dimensional sparse signal from compressed measurements corrupted by outliers. A new sparse Bayesian learning method is developed for robust compressed sensing. The basic idea of the proposed method is to identify and remove the outliers from sparse signal recovery. To automatically identify the outliers, we employ a set of binary indicator hyperparameters to indicate which observations are outliers. These indicator hyperparameters are treated as random variables and assigned a beta process prior such that their values are confined to be binary. In addition, a Gaussian-inverse Gamma prior is imposed on the sparse signal to promote sparsity. Based on this hierarchical prior model, we develop a variational Bayesian method to estimate the indicator hyperparameters as well as the sparse signal. Simulation results show that the proposed method achieves a substantial performance improvement over existing robust compressed sensing techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge