Covariant-Contravariant Refinement Modal $μ$-calculus

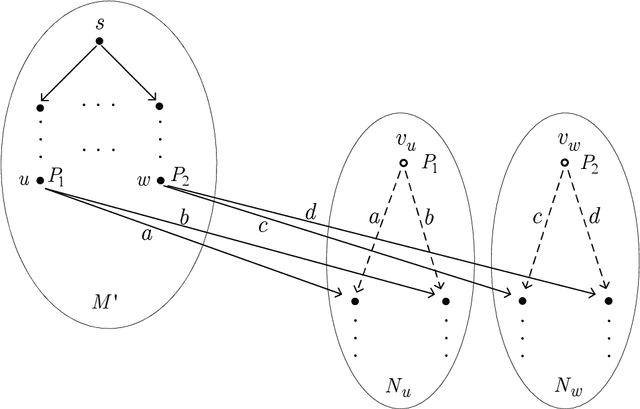
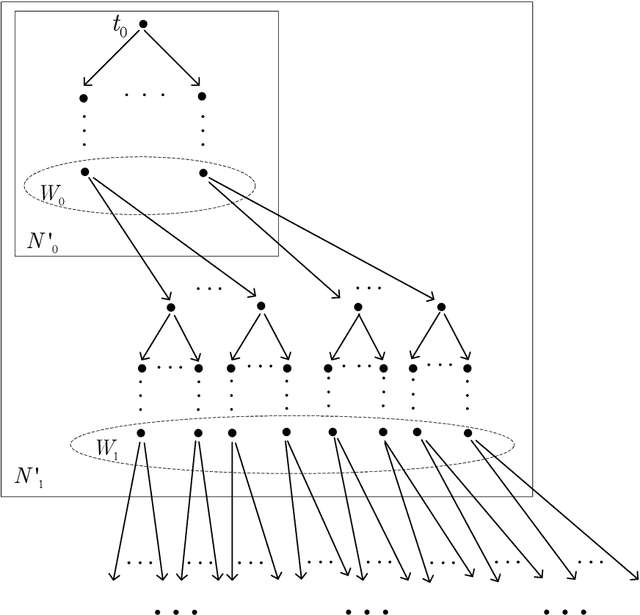
The notion of covariant-contravariant refinement (CC-refinement, for short) is a generalization of the notions of bisimulation, simulation and refinement. This paper introduces CC-refinement modal $\mu$-calculus (CCRML$^{\mu}$) obtained from the modal $\mu$-calculus system K$^{\mu}$ by adding CC-refinement quantifiers, establishes an axiom system for CCRML$^{\mu}$ and explores the important properties: soundness, completeness and decidability of this axiom system. The language of CCRML$^{\mu}$ may be considered as a specification language for describing the properties of a system referring to reactive and generative actions. It may be used to formalize some interesting problems in the field of formal methods.

A calculus for epistemic interactions

It plays a central role in intelligent agent systems to model agent's epistemic state and its change. To this end, some formal systems have been presented. Among them, epistemic logics focus on logic laws of different epistemic attributes (e.g., knowledge, belief, common knowledge, etc) and epistemic actions (e.g., public announcement, private announcement, asynchronous announcement, etc). All these systems do not involve the interactive behaviours between an agent and its environment. Through enriching the well-known $\pi$-calculus, this paper presents the e-calculus, which provides a concept framework to model epistemic interactions between agents with epistemic states. Unlike usual process calculus, all systems in the e-calculus are always arranged to run at an epistemic state. To formalize epistemic states abstractly, a group of postulates on them are presented. Moreover, based on these postulates, the behaviour theory of the e-calculus is developed in two different viewpoints.