Covariant-Contravariant Refinement Modal $μ$-calculus
Paper and Code
Aug 05, 2022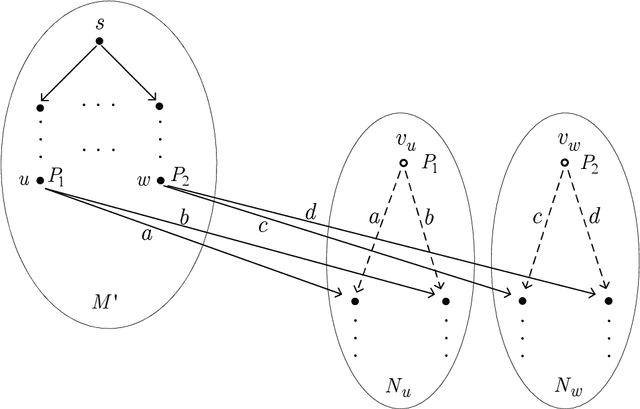
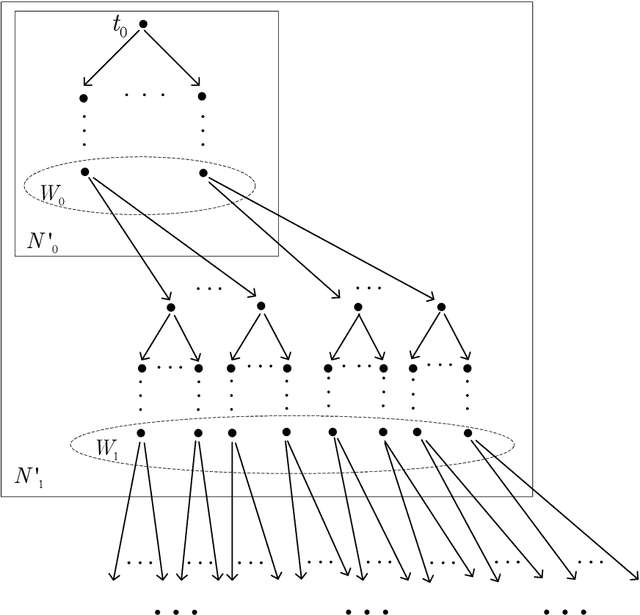
The notion of covariant-contravariant refinement (CC-refinement, for short) is a generalization of the notions of bisimulation, simulation and refinement. This paper introduces CC-refinement modal $\mu$-calculus (CCRML$^{\mu}$) obtained from the modal $\mu$-calculus system K$^{\mu}$ by adding CC-refinement quantifiers, establishes an axiom system for CCRML$^{\mu}$ and explores the important properties: soundness, completeness and decidability of this axiom system. The language of CCRML$^{\mu}$ may be considered as a specification language for describing the properties of a system referring to reactive and generative actions. It may be used to formalize some interesting problems in the field of formal methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge