Horst C. Samulowitz
Toward Theoretical Guidance for Two Common Questions in Practical Cross-Validation based Hyperparameter Selection
Jan 12, 2023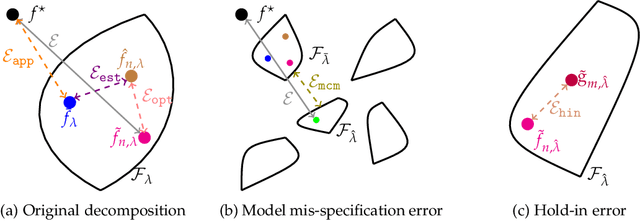

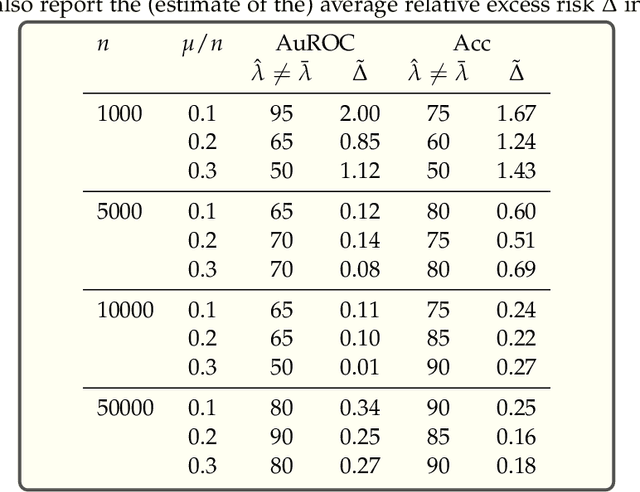
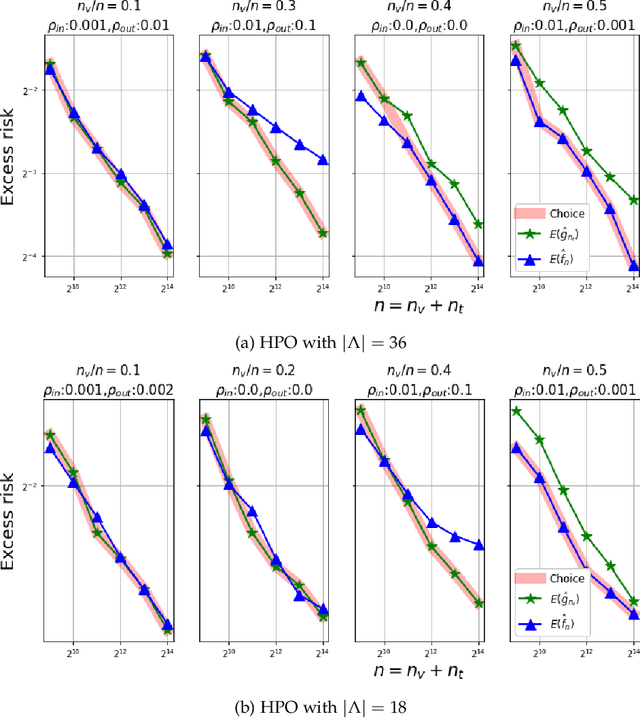
Abstract:We show, to our knowledge, the first theoretical treatments of two common questions in cross-validation based hyperparameter selection: (1) After selecting the best hyperparameter using a held-out set, we train the final model using {\em all} of the training data -- since this may or may not improve future generalization error, should one do this? (2) During optimization such as via SGD (stochastic gradient descent), we must set the optimization tolerance $\rho$ -- since it trades off predictive accuracy with computation cost, how should one set it? Toward these problems, we introduce the {\em hold-in risk} (the error due to not using the whole training data), and the {\em model class mis-specification risk} (the error due to having chosen the wrong model class) in a theoretical view which is simple, general, and suggests heuristics that can be used when faced with a dataset instance. In proof-of-concept studies in synthetic data where theoretical quantities can be controlled, we show that these heuristics can, respectively, (1) always perform at least as well as always performing retraining or never performing retraining, (2) either improve performance or reduce computational overhead by $2\times$ with no loss in predictive performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge