Approximate Gibbs Sampler for Efficient Inference of Hierarchical Bayesian Models for Grouped Count Data

Hierarchical Bayesian Poisson regression models (HBPRMs) provide a flexible modeling approach of the relationship between predictors and count response variables. The applications of HBPRMs to large-scale datasets require efficient inference algorithms due to the high computational cost of inferring many model parameters based on random sampling. Although Markov Chain Monte Carlo (MCMC) algorithms have been widely used for Bayesian inference, sampling using this class of algorithms is time-consuming for applications with large-scale data and time-sensitive decision-making, partially due to the non-conjugacy of many models. To overcome this limitation, this research develops an approximate Gibbs sampler (AGS) to efficiently learn the HBPRMs while maintaining the inference accuracy. In the proposed sampler, the data likelihood is approximated with Gaussian distribution such that the conditional posterior of the coefficients has a closed-form solution. Numerical experiments using real and synthetic datasets with small and large counts demonstrate the superior performance of AGS in comparison to the state-of-the-art sampling algorithm, especially for large datasets.

A Bayesian Approach to Reconstructing Interdependent Infrastructure Networks from Cascading Failures

Analyzing the behavior of complex interdependent networks requires complete information about the network topology and the interdependent links across networks. For many applications such as critical infrastructure systems, understanding network interdependencies is crucial to anticipate cascading failures and plan for disruptions. However, data on the topology of individual networks are often publicly unavailable due to privacy and security concerns. Additionally, interdependent links are often only revealed in the aftermath of a disruption as a result of cascading failures. We propose a scalable nonparametric Bayesian approach to reconstruct the topology of interdependent infrastructure networks from observations of cascading failures. Metropolis-Hastings algorithm coupled with the infrastructure-dependent proposal are employed to increase the efficiency of sampling possible graphs. Results of reconstructing a synthetic system of interdependent infrastructure networks demonstrate that the proposed approach outperforms existing methods in both accuracy and computational time. We further apply this approach to reconstruct the topology of one synthetic and two real-world systems of interdependent infrastructure networks, including gas-power-water networks in Shelby County, TN, USA, and an interdependent system of power-water networks in Italy, to demonstrate the general applicability of the approach.

Learning Incident Prediction Models Over Large Geographical Areas for Emergency Response Systems

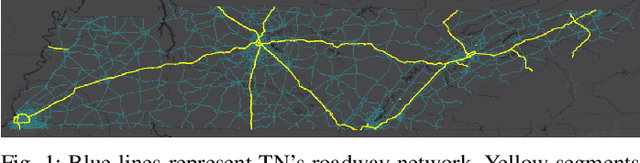
Principled decision making in emergency response management necessitates the use of statistical models that predict the spatial-temporal likelihood of incident occurrence. These statistical models are then used for proactive stationing which allocates first responders across the spatial area in order to reduce overall response time. Traditional methods that simply aggregate past incidents over space and time fail to make useful short-term predictions when the spatial region is large and focused on fine-grained spatial entities like interstate highway networks. This is partially due to the sparsity of incidents with respect to the area in consideration. Further, accidents are affected by several covariates, and collecting, cleaning, and managing multiple streams of data from various sources is challenging for large spatial areas. In this paper, we highlight how this problem is being solved for the state of Tennessee, a state in the USA with a total area of over 100,000 sq. km. Our pipeline, based on a combination of synthetic resampling, non-spatial clustering, and learning from data can efficiently forecast the spatial and temporal dynamics of accident occurrence, even under sparse conditions. In the paper, we describe our pipeline that uses data related to roadway geometry, weather, historical accidents, and real-time traffic congestion to aid accident forecasting. To understand how our forecasting model can affect allocation and dispatch, we improve upon a classical resource allocation approach. Experimental results show that our approach can significantly reduce response times in the field in comparison with current approaches followed by first responders.