Some Problems for Convex Bayesians

We discuss problems for convex Bayesian decision making and uncertainty representation. These include the inability to accommodate various natural and useful constraints and the possibility of an analog of the classical Dutch Book being made against an agent behaving in accordance with convex Bayesian prescriptions. A more general set-based Bayesianism may be as tractable and would avoid the difficulties we raise.

Choosing Among Interpretations of Probability

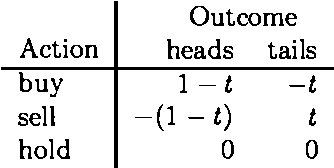
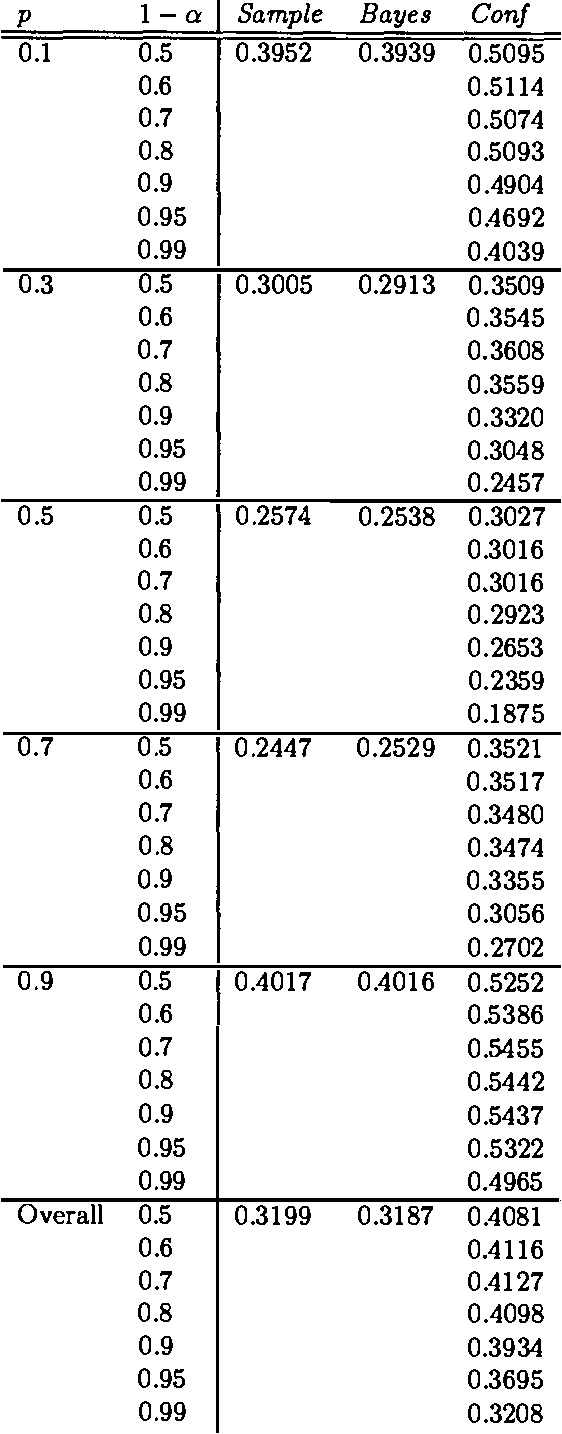
There is available an ever-increasing variety of procedures for managing uncertainty. These methods are discussed in the literature of artificial intelligence, as well as in the literature of philosophy of science. Heretofore these methods have been evaluated by intuition, discussion, and the general philosophical method of argument and counterexample. Almost any method of uncertainty management will have the property that in the long run it will deliver numbers approaching the relative frequency of the kinds of events at issue. To find a measure that will provide a meaningful evaluation of these treatments of uncertainty, we must look, not at the long run, but at the short or intermediate run. Our project attempts to develop such a measure in terms of short or intermediate length performance. We represent the effects of practical choices by the outcomes of bets offered to agents characterized by two uncertainty management approaches: the subjective Bayesian approach and the Classical confidence interval approach. Experimental evaluation suggests that the confidence interval approach can outperform the subjective approach in the relatively short run.

Evaluating Defaults

We seek to find normative criteria of adequacy for nonmonotonic logic similar to the criterion of validity for deductive logic. Rather than stipulating that the conclusion of an inference be true in all models in which the premises are true, we require that the conclusion of a nonmonotonic inference be true in ``almost all'' models of a certain sort in which the premises are true. This ``certain sort'' specification picks out the models that are relevant to the inference, taking into account factors such as specificity and vagueness, and previous inferences. The frequencies characterizing the relevant models reflect known frequencies in our actual world. The criteria of adequacy for a default inference can be extended by thresholding to criteria of adequacy for an extension. We show that this avoids the implausibilities that might otherwise result from the chaining of default inferences. The model proportions, when construed in terms of frequencies, provide a verifiable grounding of default rules, and can become the basis for generating default rules from statistics.