Interactive Cost Configuration Over Decision Diagrams

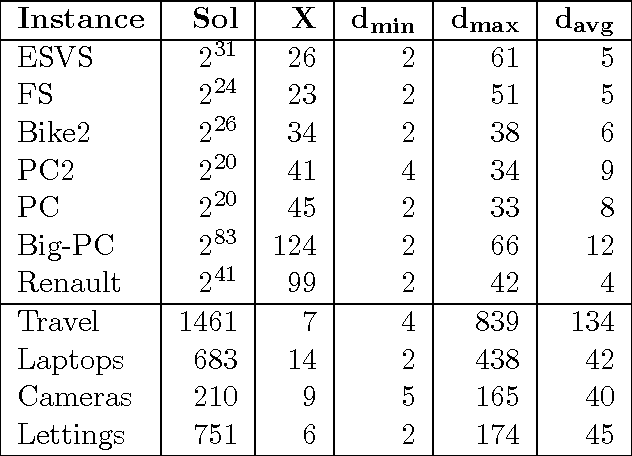
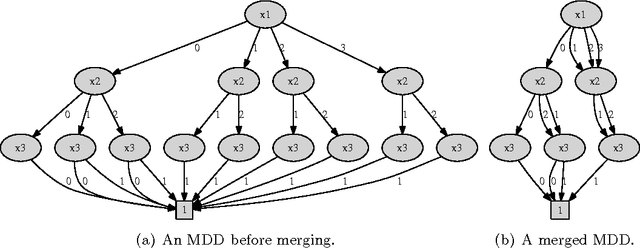
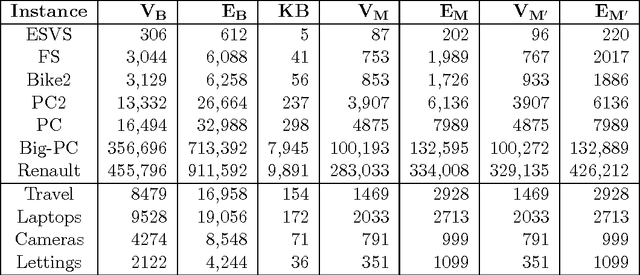
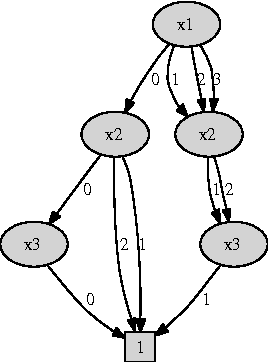
In many AI domains such as product configuration, a user should interactively specify a solution that must satisfy a set of constraints. In such scenarios, offline compilation of feasible solutions into a tractable representation is an important approach to delivering efficient backtrack-free user interaction online. In particular,binary decision diagrams (BDDs) have been successfully used as a compilation target for product and service configuration. In this paper we discuss how to extend BDD-based configuration to scenarios involving cost functions which express user preferences. We first show that an efficient, robust and easy to implement extension is possible if the cost function is additive, and feasible solutions are represented using multi-valued decision diagrams (MDDs). We also discuss the effect on MDD size if the cost function is non-additive or if it is encoded explicitly into MDD. We then discuss interactive configuration in the presence of multiple cost functions. We prove that even in its simplest form, multiple-cost configuration is NP-hard in the input MDD. However, for solving two-cost configuration we develop a pseudo-polynomial scheme and a fully polynomial approximation scheme. The applicability of our approach is demonstrated through experiments over real-world configuration models and product-catalogue datasets. Response times are generally within a fraction of a second even for very large instances.

Calculating Valid Domains for BDD-Based Interactive Configuration

In these notes we formally describe the functionality of Calculating Valid Domains from the BDD representing the solution space of valid configurations. The formalization is largely based on the CLab configuration framework.

Generic Global Constraints based on MDDs

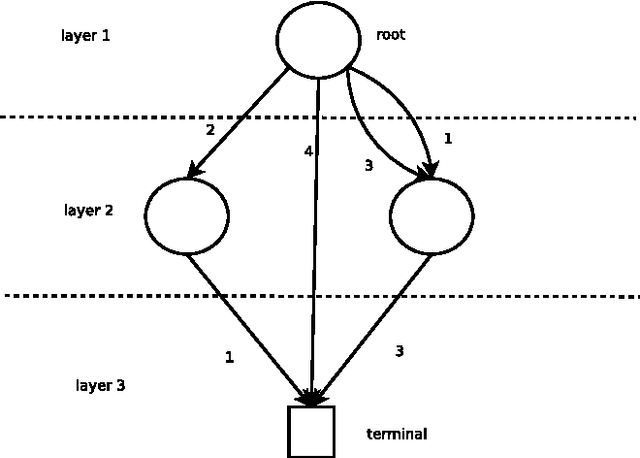
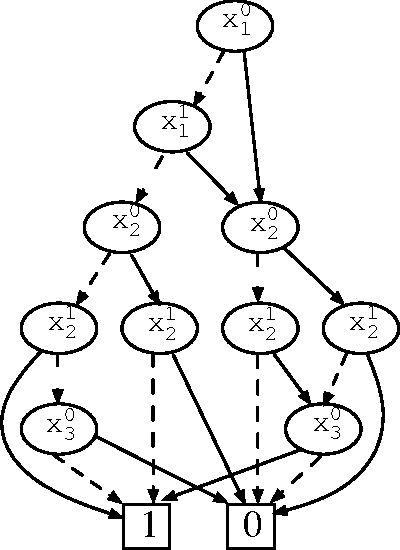
Constraint Programming (CP) has been successfully applied to both constraint satisfaction and constraint optimization problems. A wide variety of specialized global constraints provide critical assistance in achieving a good model that can take advantage of the structure of the problem in the search for a solution. However, a key outstanding issue is the representation of 'ad-hoc' constraints that do not have an inherent combinatorial nature, and hence are not modeled well using narrowly specialized global constraints. We attempt to address this issue by considering a hybrid of search and compilation. Specifically we suggest the use of Reduced Ordered Multi-Valued Decision Diagrams (ROMDDs) as the supporting data structure for a generic global constraint. We give an algorithm for maintaining generalized arc consistency (GAC) on this constraint that amortizes the cost of the GAC computation over a root-to-leaf path in the search tree without requiring asymptotically more space than used for the MDD. Furthermore we present an approach for incrementally maintaining the reduced property of the MDD during the search, and show how this can be used for providing domain entailment detection. Finally we discuss how to apply our approach to other similar data structures such as AOMDDs and Case DAGs. The technique used can be seen as an extension of the GAC algorithm for the regular language constraint on finite length input.

Interactive Configuration by Regular String Constraints

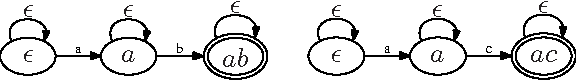
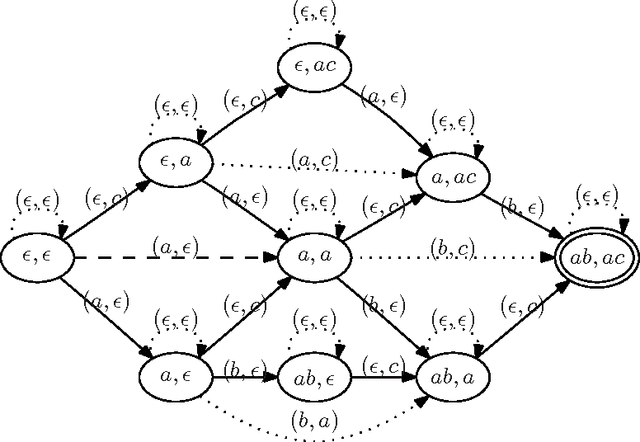
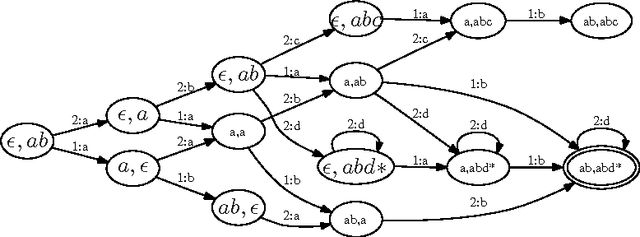
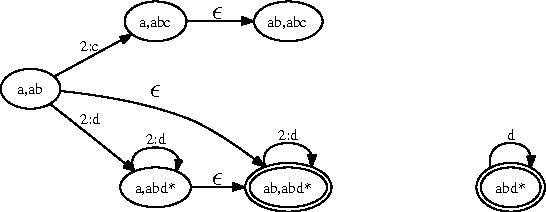
A product configurator which is complete, backtrack free and able to compute the valid domains at any state of the configuration can be constructed by building a Binary Decision Diagram (BDD). Despite the fact that the size of the BDD is exponential in the number of variables in the worst case, BDDs have proved to work very well in practice. Current BDD-based techniques can only handle interactive configuration with small finite domains. In this paper we extend the approach to handle string variables constrained by regular expressions. The user is allowed to change the strings by adding letters at the end of the string. We show how to make a data structure that can perform fast valid domain computations given some assignment on the set of string variables. We first show how to do this by using one large DFA. Since this approach is too space consuming to be of practical use, we construct a data structure that simulates the large DFA and in most practical cases are much more space efficient. As an example a configuration problem on $n$ string variables with only one solution in which each string variable is assigned to a value of length of $k$ the former structure will use $\Omega(k^n)$ space whereas the latter only need $O(kn)$. We also show how this framework easily can be combined with the recent BDD techniques to allow both boolean, integer and string variables in the configuration problem.

A Generic Global Constraint based on MDDs

The paper suggests the use of Multi-Valued Decision Diagrams (MDDs) as the supporting data structure for a generic global constraint. We give an algorithm for maintaining generalized arc consistency (GAC) on this constraint that amortizes the cost of the GAC computation over a root-to-terminal path in the search tree. The technique used is an extension of the GAC algorithm for the regular language constraint on finite length input. Our approach adds support for skipped variables, maintains the reduced property of the MDD dynamically and provides domain entailment detection. Finally we also show how to adapt the approach to constraint types that are closely related to MDDs, such as AOMDDs and Case DAGs.