Interactive Configuration by Regular String Constraints
Paper and Code
Dec 12, 2006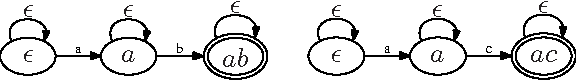
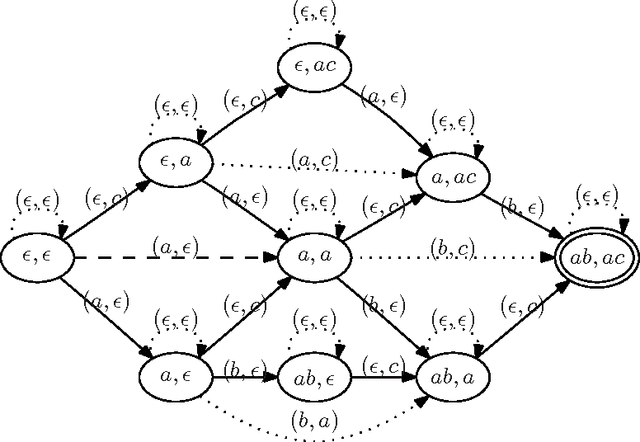
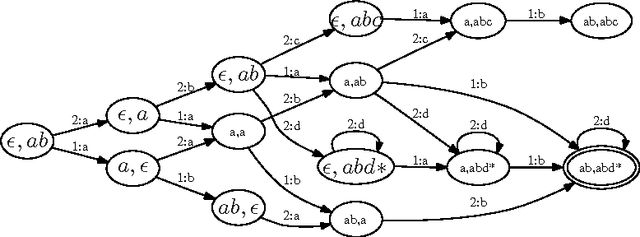
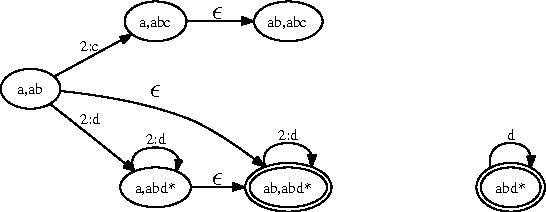
A product configurator which is complete, backtrack free and able to compute the valid domains at any state of the configuration can be constructed by building a Binary Decision Diagram (BDD). Despite the fact that the size of the BDD is exponential in the number of variables in the worst case, BDDs have proved to work very well in practice. Current BDD-based techniques can only handle interactive configuration with small finite domains. In this paper we extend the approach to handle string variables constrained by regular expressions. The user is allowed to change the strings by adding letters at the end of the string. We show how to make a data structure that can perform fast valid domain computations given some assignment on the set of string variables. We first show how to do this by using one large DFA. Since this approach is too space consuming to be of practical use, we construct a data structure that simulates the large DFA and in most practical cases are much more space efficient. As an example a configuration problem on $n$ string variables with only one solution in which each string variable is assigned to a value of length of $k$ the former structure will use $\Omega(k^n)$ space whereas the latter only need $O(kn)$. We also show how this framework easily can be combined with the recent BDD techniques to allow both boolean, integer and string variables in the configuration problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge