Stochastic Reservoir Computers

Reservoir computing is a form of machine learning that utilizes nonlinear dynamical systems to perform complex tasks in a cost-effective manner when compared to typical neural networks. Many recent advancements in reservoir computing, in particular quantum reservoir computing, make use of reservoirs that are inherently stochastic. However, the theoretical justification for using these systems has not yet been well established. In this paper, we investigate the universality of stochastic reservoir computers, in which we use a stochastic system for reservoir computing using the probabilities of each reservoir state as the readout instead of the states themselves. In stochastic reservoir computing, the number of distinct states of the entire reservoir computer can potentially scale exponentially with the size of the reservoir hardware, offering the advantage of compact device size. We prove that classes of stochastic echo state networks, and therefore the class of all stochastic reservoir computers, are universal approximating classes. We also investigate the performance of two practical examples of stochastic reservoir computers in classification and chaotic time series prediction. While shot noise is a limiting factor in the performance of stochastic reservoir computing, we show significantly improved performance compared to a deterministic reservoir computer with similar hardware in cases where the effects of noise are small.

Improving the Performance of Echo State Networks Through Feedback

Reservoir computing, using nonlinear dynamical systems, offers a cost-effective alternative to neural networks for complex tasks involving processing of sequential data, time series modeling, and system identification. Echo state networks (ESNs), a type of reservoir computer, mirror neural networks but simplify training. They apply fixed, random linear transformations to the internal state, followed by nonlinear changes. This process, guided by input signals and linear regression, adapts the system to match target characteristics, reducing computational demands. A potential drawback of ESNs is that the fixed reservoir may not offer the complexity needed for specific problems. While directly altering (training) the internal ESN would reintroduce the computational burden, an indirect modification can be achieved by redirecting some output as input. This feedback can influence the internal reservoir state, yielding ESNs with enhanced complexity suitable for broader challenges. In this paper, we demonstrate that by feeding some component of the reservoir state back into the network through the input, we can drastically improve upon the performance of a given ESN. We rigorously prove that, for any given ESN, feedback will almost always improve the accuracy of the output. For a set of three tasks, each representing different problem classes, we find that with feedback the average error measures are reduced by $30\%-60\%$. Remarkably, feedback provides at least an equivalent performance boost to doubling the initial number of computational nodes, a computationally expensive and technologically challenging alternative. These results demonstrate the broad applicability and substantial usefulness of this feedback scheme.

Temporal Information Processing on Noisy Quantum Computers

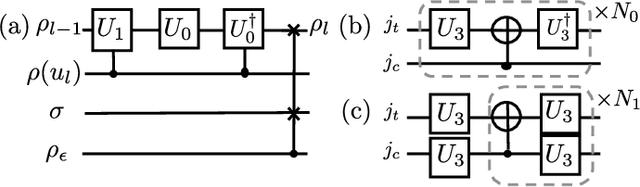
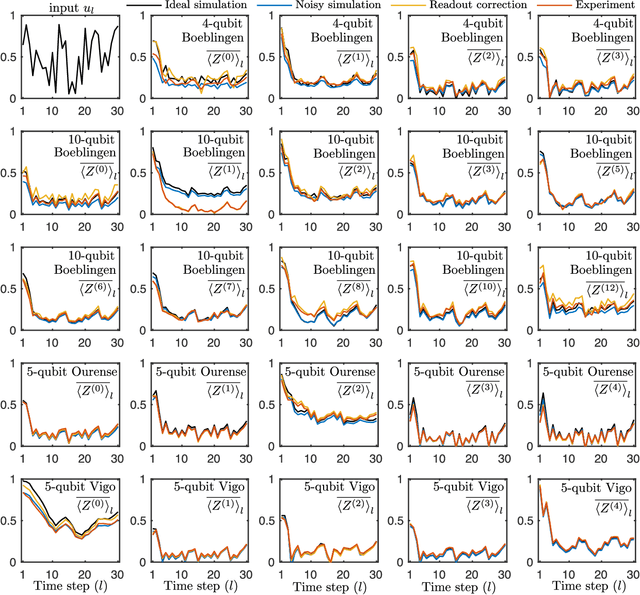
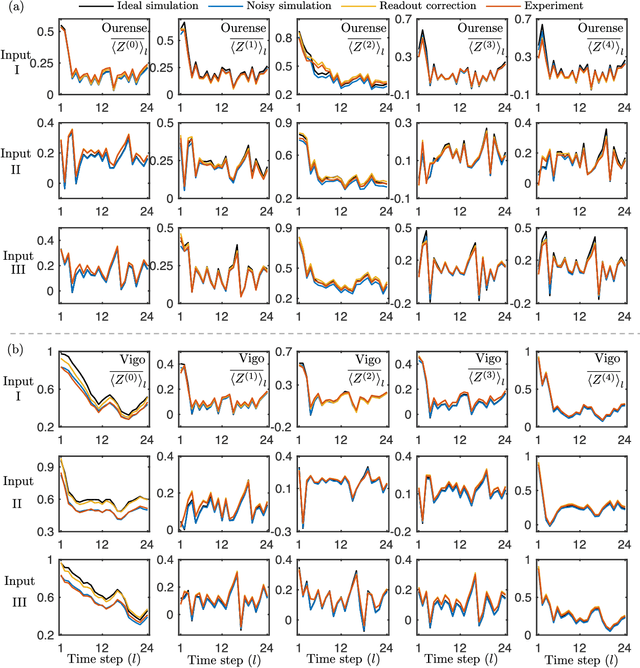
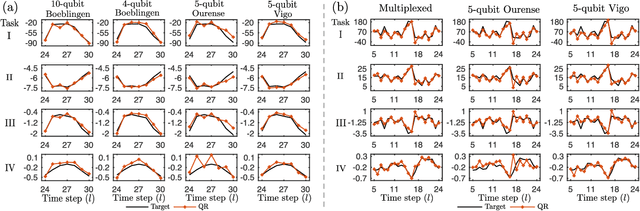
The combination of machine learning and quantum computing has emerged as a promising approach for addressing previously untenable problems. Reservoir computing is a state-of-the-art machine learning paradigm that utilizes nonlinear dynamical systems for temporal information processing, whose state-space dimension plays a key role in the performance. Here we propose a quantum reservoir system that harnesses complex dissipative quantum dynamics and the exponentially large quantum state-space. Our proposal is readily implementable on available noisy gate-model quantum processors and possesses universal computational power for approximating nonlinear short-term memory maps, important in applications such as neural modeling, speech recognition and natural language processing. We experimentally demonstrate on superconducting quantum computers that small and noisy quantum reservoirs can tackle high-order nonlinear temporal tasks. Our theoretical and experimental results pave the way for attractive temporal processing applications of near-term gate-model quantum computers of increasing fidelity but without quantum error correction, signifying the potential of these devices for wider applications beyond static classification and regression tasks in interdisciplinary areas.

Learning Nonlinear Input-Output Maps with Dissipative Quantum Systems

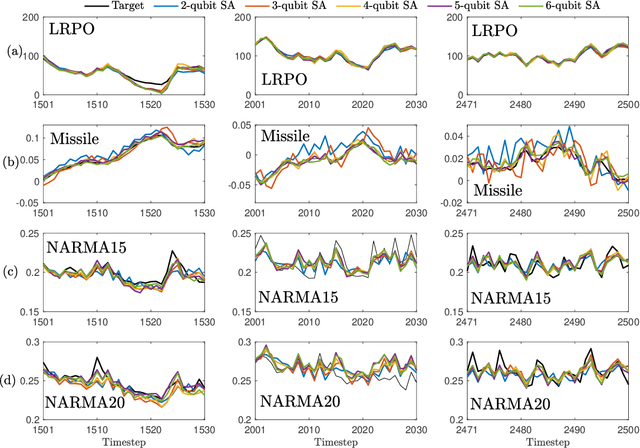
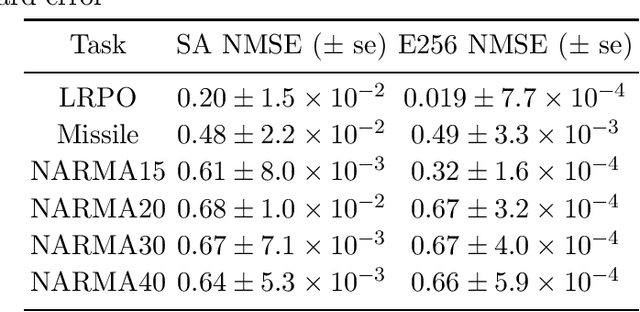
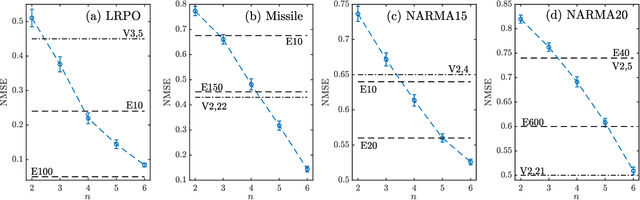
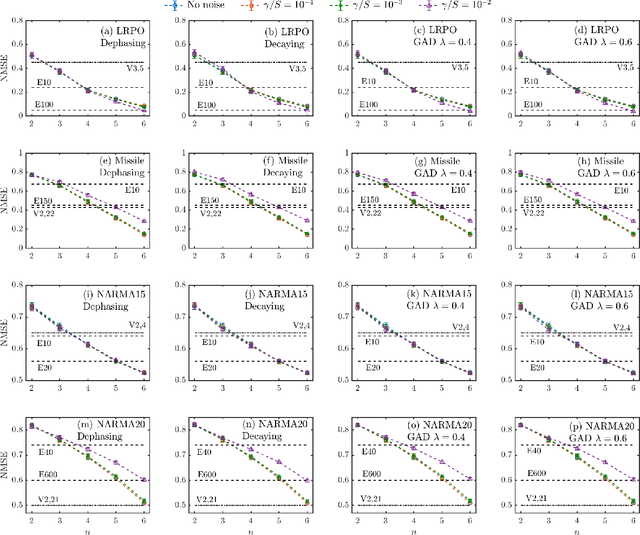
In this paper, we develop a theory of learning nonlinear input-output maps with fading memory by dissipative quantum systems, as a quantum counterpart of the theory of approximating such maps using classical dynamical systems. The theory identifies the properties required for a class of dissipative quantum systems to be {\em universal}, in that any input-output map with fading memory can be approximated arbitrarily closely by an element of this class. We then introduce an example class of dissipative quantum systems that is provably universal. Numerical experiments illustrate that with a small number of qubits, this class can achieve comparable performance to classical learning schemes with a large number of tunable parameters. Further numerical analysis suggests that the exponentially increasing Hilbert space presents a potential resource for dissipative quantum systems to surpass classical learning schemes for input-output maps.