Heiko Gimperlein
Efficient quantitative assessment of robot swarms: coverage and targeting Lévy strategies
Feb 14, 2022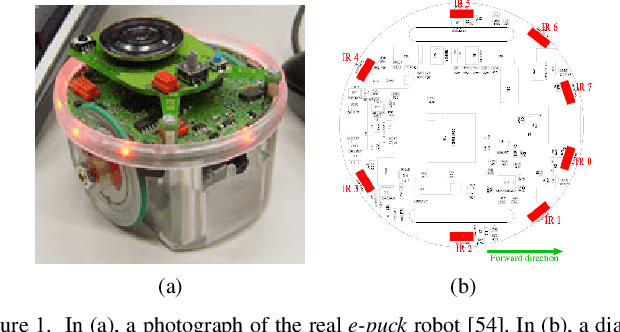

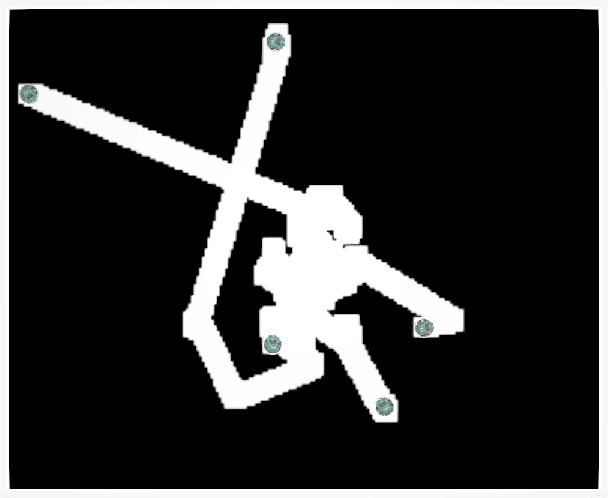
Abstract:Biologically inspired strategies have long been adapted to swarm robotic systems, including biased random walks, reaction to chemotactic cues and long-range coordination. In this paper we apply analysis tools developed for modeling biological systems, such as continuum descriptions, to the efficient quantitative characterization of robot swarms. As an illustration, both Brownian and L\'{e}vy strategies with a characteristic long-range movement are discussed. As a result we obtain computationally fast methods for the optimization of robot movement laws to achieve a prescribed collective behavior. We show how to compute performance metrics like coverage and hitting times, and illustrate the accuracy and efficiency of our approach for area coverage and search problems. Comparisons between the continuum model and robotic simulations confirm the quantitative agreement and speed up of our approach. Results confirm and quantify the advantage of L\'{e}vy strategies over Brownian motion for search and area coverage problems in swarm robotics.
Interacting particles with Lévy strategies: limits of transport equations for swarm robotic systems
Nov 13, 2018

Abstract:L\'{e}vy robotic systems combine superdiffusive random movement with emergent collective behaviour from local communication and alignment in order to find rare targets or track objects. In this article we derive macroscopic fractional PDE descriptions from the movement strategies of the individual robots. Starting from a kinetic equation which describes the movement of robots based on alignment, collisions and occasional long distance runs according to a L\'{e}vy distribution, we obtain a system of evolution equations for the fractional diffusion for long times. We show that the system allows efficient parameter studies for a search problem, addressing basic questions like the optimal number of robots needed to cover an area in a certain time. For shorter times, in the hyperbolic limit of the kinetic equation, the PDE model is dominated by alignment, irrespective of the long range movement. This is in agreement with previous results in swarming of self-propelled particles. The article indicates the novel and quantitative modeling opportunities which swarm robotic systems provide for the study of both emergent collective behaviour and anomalous diffusion, on the respective time scales.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge