Offline Policy Learning with Weight Clipping and Heaviside Composite Optimization

Offline policy learning aims to use historical data to learn an optimal personalized decision rule. In the standard estimate-then-optimize framework, reweighting-based methods (e.g., inverse propensity weighting or doubly robust estimators) are widely used to produce unbiased estimates of policy values. However, when the propensity scores of some treatments are small, these reweighting-based methods suffer from high variance in policy value estimation, which may mislead the downstream policy optimization and yield a learned policy with inferior value. In this paper, we systematically develop an offline policy learning algorithm based on a weight-clipping estimator that truncates small propensity scores via a clipping threshold chosen to minimize the mean squared error (MSE) in policy value estimation. Focusing on linear policies, we address the bilevel and discontinuous objective induced by weight-clipping-based policy optimization by reformulating the problem as a Heaviside composite optimization problem, which provides a rigorous computational framework. The reformulated policy optimization problem is then solved efficiently using the progressive integer programming method, making practical policy learning tractable. We establish an upper bound for the suboptimality of the proposed algorithm, which reveals how the reduction in MSE of policy value estimation, enabled by our proposed weight-clipping estimator, leads to improved policy learning performance.

LLM for Large-Scale Optimization Model Auto-Formulation: A Lightweight Few-Shot Learning Approach

Large-scale optimization is a key backbone of modern business decision-making. However, building these models is often labor-intensive and time-consuming. We address this by proposing LEAN-LLM-OPT, a LightwEight AgeNtic workflow construction framework for LLM-assisted large-scale OPTimization auto-formulation. LEAN-LLM-OPT takes as input a problem description together with associated datasets and orchestrates a team of LLM agents to produce an optimization formulation. Specifically, upon receiving a query, two upstream LLM agents dynamically construct a workflow that specifies, step-by-step, how optimization models for similar problems can be formulated. A downstream LLM agent then follows this workflow to generate the final output. Leveraging LLMs' text-processing capabilities and common modeling practices, the workflow decomposes the modeling task into a sequence of structured sub-tasks and offloads mechanical data-handling operations to auxiliary tools. This design alleviates the downstream agent's burden related to planning and data handling, allowing it to focus on the most challenging components that cannot be readily standardized. Extensive simulations show that LEAN-LLM-OPT, instantiated with GPT-4.1 and the open source gpt-oss-20B, achieves strong performance on large-scale optimization modeling tasks and is competitive with state-of-the-art approaches. In addition, in a Singapore Airlines choice-based revenue management use case, LEAN-LLM-OPT demonstrates practical value by achieving leading performance across a range of scenarios. Along the way, we introduce Large-Scale-OR and Air-NRM, the first comprehensive benchmarks for large-scale optimization auto-formulation. The code and data of this work is available at https://github.com/CoraLiang01/lean-llm-opt.

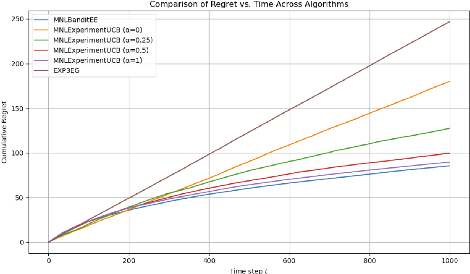
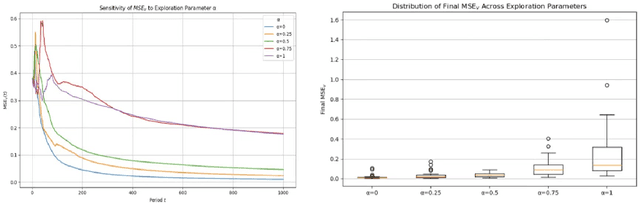
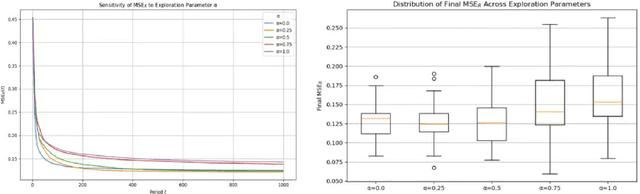
On Pareto Optimality for the Multinomial Logistic Bandit

We provide a new online learning algorithm for tackling the Multinomial Logit Bandit (MNL-Bandit) problem. Despite the challenges posed by the combinatorial nature of the MNL model, we develop a novel Upper Confidence Bound (UCB)-based method that achieves Pareto optimality by balancing regret minimization and estimation error of the assortment revenues and the MNL parameters. We develop theoretical guarantees characterizing the tradeoff between regret and estimation error for the MNL-Bandit problem through information-theoretic bounds, and propose a modified UCB algorithm that incorporates forced exploration to improve parameter estimation accuracy while maintaining low regret. Our analysis sheds critical insights into how to optimally balance the collected revenues and the treatment estimation in dynamic assortment optimization.

Online Resource Allocation with Non-Stationary Customers

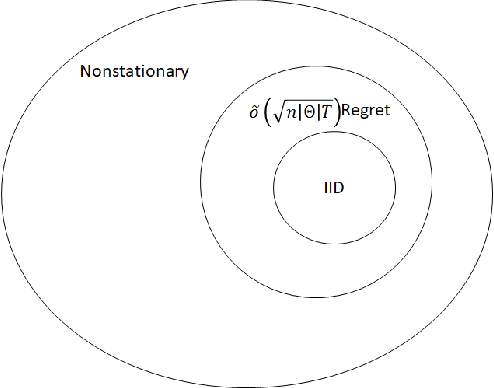
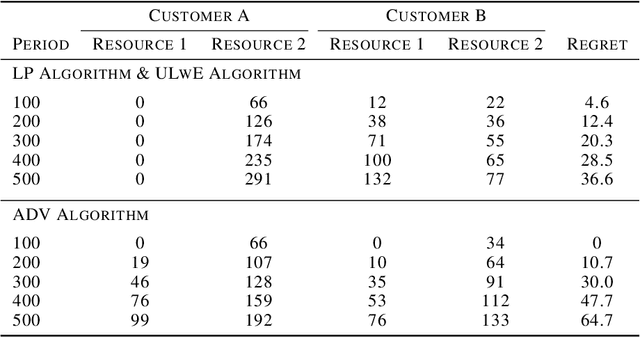
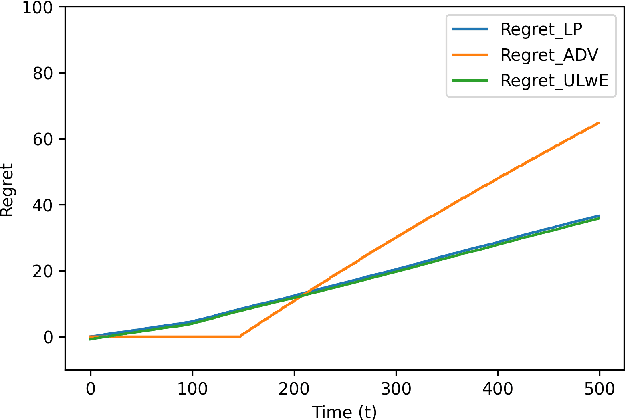
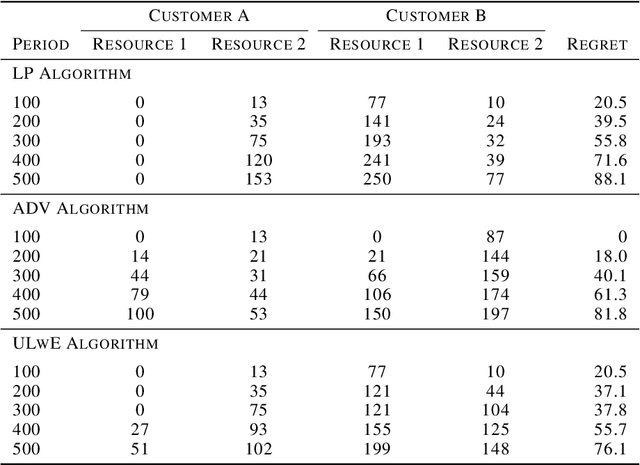
We propose a novel algorithm for online resource allocation with non-stationary customer arrivals and unknown click-through rates. We assume multiple types of customers arrive in a nonstationary stochastic fashion, with unknown arrival rates in each period, and that customers' click-through rates are unknown and can only be learned online. By leveraging results from the stochastic contextual bandit with knapsack and online matching with adversarial arrivals, we develop an online scheme to allocate the resources to nonstationary customers. We prove that under mild conditions, our scheme achieves a ``best-of-both-world'' result: the scheme has a sublinear regret when the customer arrivals are near-stationary, and enjoys an optimal competitive ratio under general (non-stationary) customer arrival distributions. Finally, we conduct extensive numerical experiments to show our approach generates near-optimal revenues for all different customer scenarios.