Towards Robust Foundation Models for Digital Pathology

Biomedical Foundation Models (FMs) are rapidly transforming AI-enabled healthcare research and entering clinical validation. However, their susceptibility to learning non-biological technical features -- including variations in surgical/endoscopic techniques, laboratory procedures, and scanner hardware -- poses risks for clinical deployment. We present the first systematic investigation of pathology FM robustness to non-biological features. Our work (i) introduces measures to quantify FM robustness, (ii) demonstrates the consequences of limited robustness, and (iii) proposes a framework for FM robustification to mitigate these issues. Specifically, we developed PathoROB, a robustness benchmark with three novel metrics, including the robustness index, and four datasets covering 28 biological classes from 34 medical centers. Our experiments reveal robustness deficits across all 20 evaluated FMs, and substantial robustness differences between them. We found that non-robust FM representations can cause major diagnostic downstream errors and clinical blunders that prevent safe clinical adoption. Using more robust FMs and post-hoc robustification considerably reduced (but did not yet eliminate) the risk of such errors. This work establishes that robustness evaluation is essential for validating pathology FMs before clinical adoption and demonstrates that future FM development must integrate robustness as a core design principle. PathoROB provides a blueprint for assessing robustness across biomedical domains, guiding FM improvement efforts towards more robust, representative, and clinically deployable AI systems that prioritize biological information over technical artifacts.

Do Histopathological Foundation Models Eliminate Batch Effects? A Comparative Study

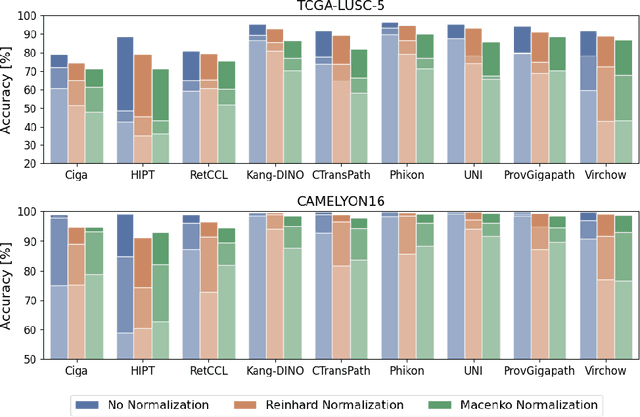
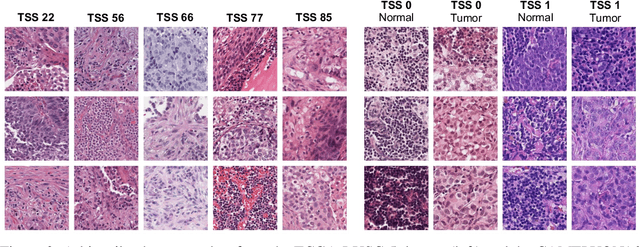
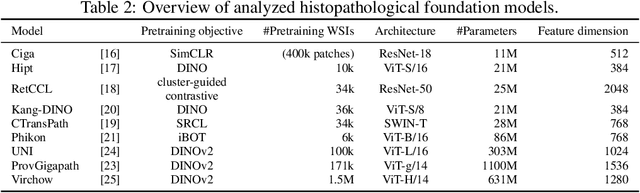
Deep learning has led to remarkable advancements in computational histopathology, e.g., in diagnostics, biomarker prediction, and outcome prognosis. Yet, the lack of annotated data and the impact of batch effects, e.g., systematic technical data differences across hospitals, hamper model robustness and generalization. Recent histopathological foundation models -- pretrained on millions to billions of images -- have been reported to improve generalization performances on various downstream tasks. However, it has not been systematically assessed whether they fully eliminate batch effects. In this study, we empirically show that the feature embeddings of the foundation models still contain distinct hospital signatures that can lead to biased predictions and misclassifications. We further find that the signatures are not removed by stain normalization methods, dominate distances in feature space, and are evident across various principal components. Our work provides a novel perspective on the evaluation of medical foundation models, paving the way for more robust pretraining strategies and downstream predictors.

Estimation of multiple mean vectors in high dimension

We endeavour to estimate numerous multi-dimensional means of various probability distributions on a common space based on independent samples. Our approach involves forming estimators through convex combinations of empirical means derived from these samples. We introduce two strategies to find appropriate data-dependent convex combination weights: a first one employing a testing procedure to identify neighbouring means with low variance, which results in a closed-form plug-in formula for the weights, and a second one determining weights via minimization of an upper confidence bound on the quadratic risk.Through theoretical analysis, we evaluate the improvement in quadratic risk offered by our methods compared to the empirical means. Our analysis focuses on a dimensional asymptotics perspective, showing that our methods asymptotically approach an oracle (minimax) improvement as the effective dimension of the data increases.We demonstrate the efficacy of our methods in estimating multiple kernel mean embeddings through experiments on both simulated and real-world datasets.

High-Dimensional Multi-Task Averaging and Application to Kernel Mean Embedding

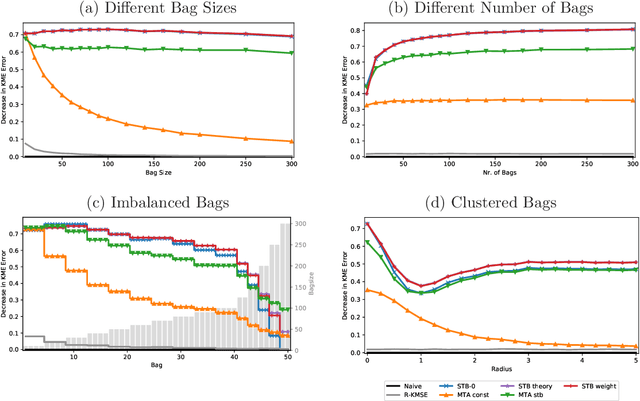
We propose an improved estimator for the multi-task averaging problem, whose goal is the joint estimation of the means of multiple distributions using separate, independent data sets. The naive approach is to take the empirical mean of each data set individually, whereas the proposed method exploits similarities between tasks, without any related information being known in advance. First, for each data set, similar or neighboring means are determined from the data by multiple testing. Then each naive estimator is shrunk towards the local average of its neighbors. We prove theoretically that this approach provides a reduction in mean squared error. This improvement can be significant when the dimension of the input space is large, demonstrating a "blessing of dimensionality" phenomenon. An application of this approach is the estimation of multiple kernel mean embeddings, which plays an important role in many modern applications. The theoretical results are verified on artificial and real world data.