Hana Alghamdi
Sliced $\mathcal{L}_2$ Distance for Colour Grading
Feb 18, 2021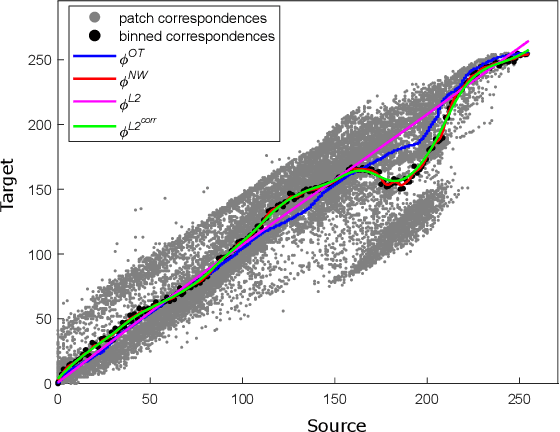
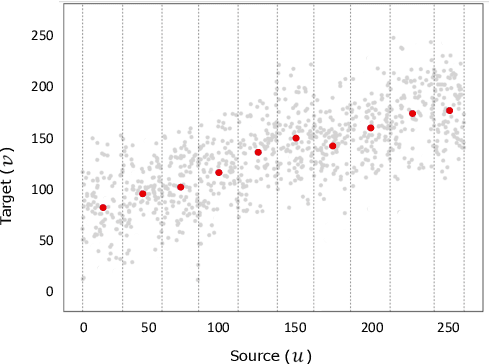
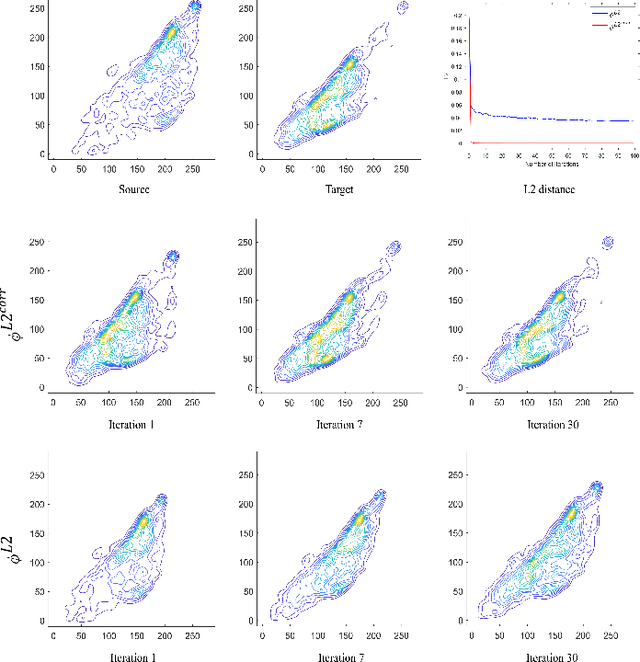
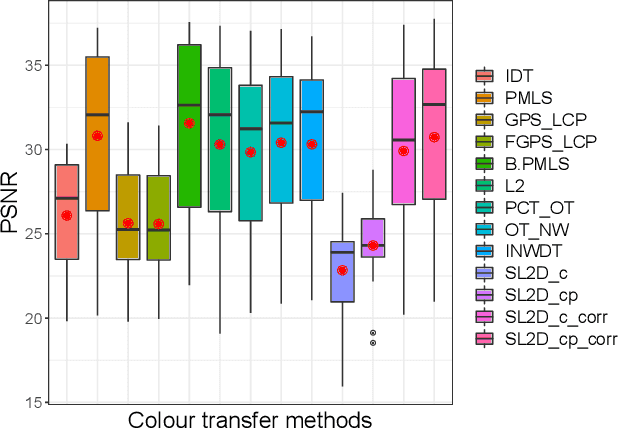
Abstract:We propose a new method with $\mathcal{L}_2$ distance that maps one $N$-dimensional distribution to another, taking into account available information about correspondences. We solve the high-dimensional problem in 1D space using an iterative projection approach. To show the potentials of this mapping, we apply it to colour transfer between two images that exhibit overlapped scenes. Experiments show quantitative and qualitative competitive results as compared with the state of the art colour transfer methods.
Iterative Nadaraya-Watson Distribution Transfer for Colour Grading
Jun 15, 2020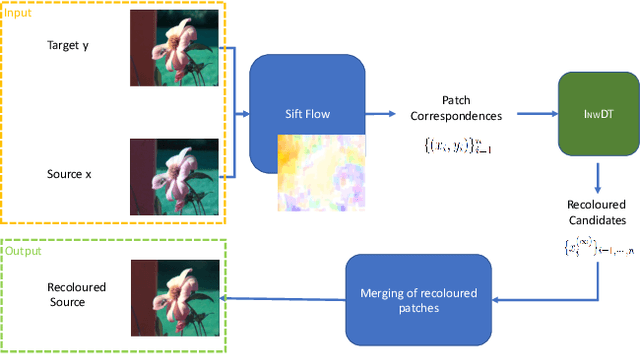
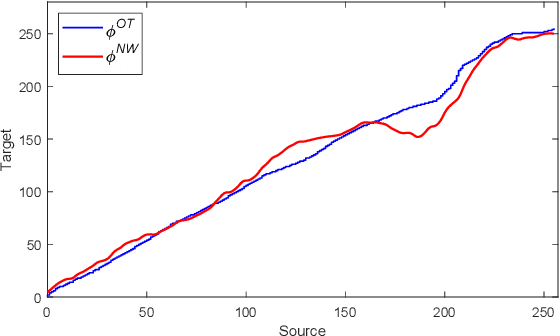
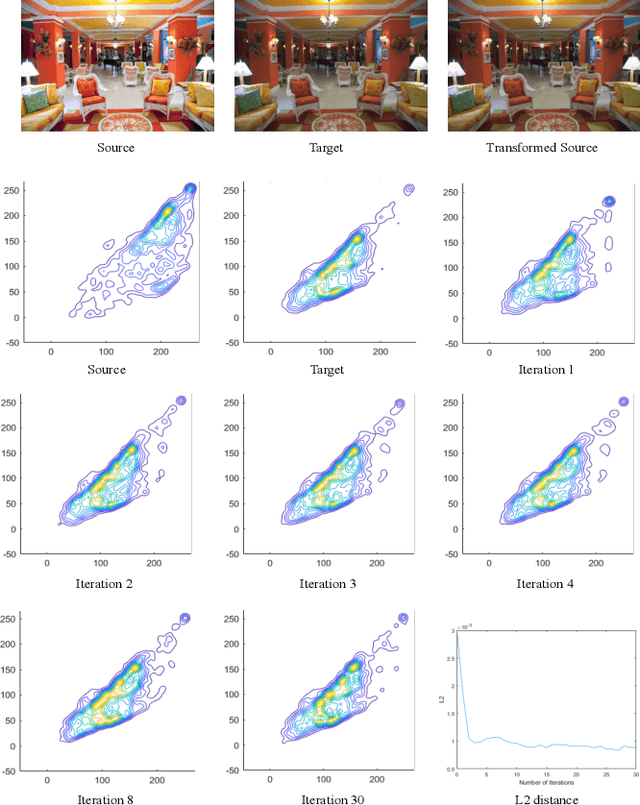
Abstract:We propose a new method with Nadaraya-Watson that maps one N-dimensional distribution to another taking into account available information about correspondences. We extend the 2D/3D problem to higher dimensions by encoding overlapping neighborhoods of data points and solve the high dimensional problem in 1D space using an iterative projection approach. To show potentials of this mapping, we apply it to colour transfer between two images that exhibit overlapped scene. Experiments show quantitative and qualitative improvements over previous state of the art colour transfer methods.
Patch based Colour Transfer using SIFT Flow
May 18, 2020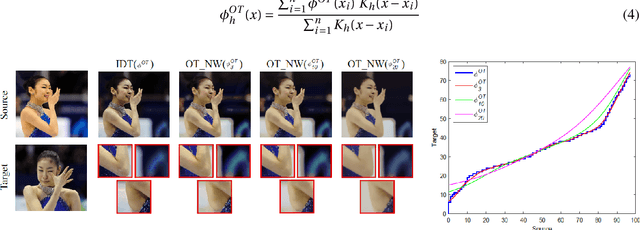
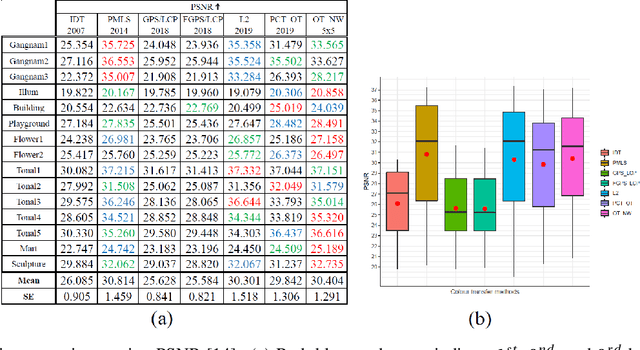
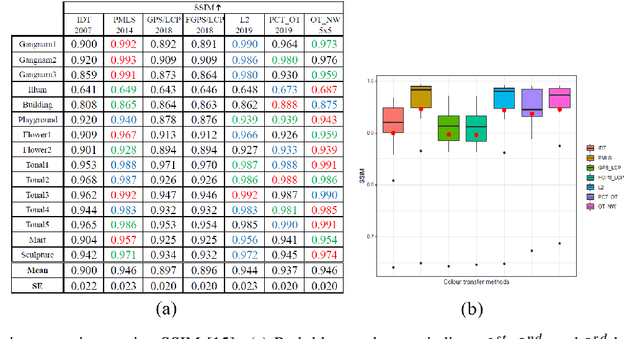

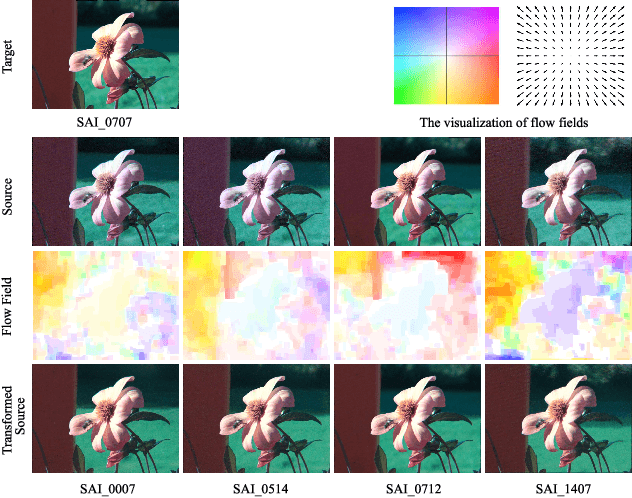
Abstract:We propose a new colour transfer method with Optimal Transport (OT) to transfer the colour of a sourceimage to match the colour of a target image of the same scene that may exhibit large motion changes betweenimages. By definition OT does not take into account any available information about correspondences whencomputing the optimal solution. To tackle this problem we propose to encode overlapping neighborhoodsof pixels using both their colour and spatial correspondences estimated using motion estimation. We solvethe high dimensional problem in 1D space using an iterative projection approach. We further introducesmoothing as part of the iterative algorithms for solving optimal transport namely Iterative DistributionTransport (IDT) and its variant the Sliced Wasserstein Distance (SWD). Experiments show quantitative andqualitative improvements over previous state of the art colour transfer methods.
Entropic Regularisation of Robust Optimal Transport
May 29, 2019
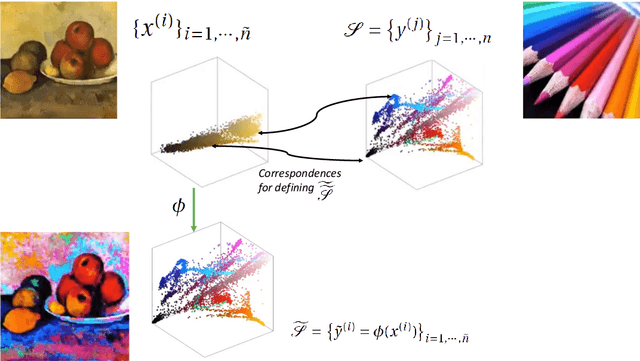
Abstract:Grogan et al [11,12] have recently proposed a solution to colour transfer by minimising the Euclidean distance L2 between two probability density functions capturing the colour distributions of two images (palette and target). It was shown to be very competitive to alternative solutions based on Optimal Transport for colour transfer. We show that in fact Grogan et al's formulation can also be understood as a new robust Optimal Transport based framework with entropy regularisation over marginals.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge