Sliced $\mathcal{L}_2$ Distance for Colour Grading
Paper and Code
Feb 18, 2021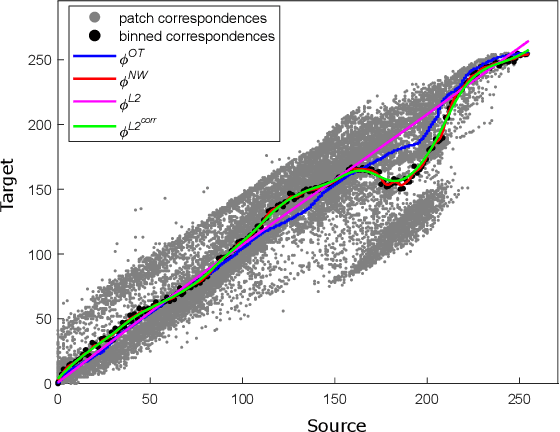
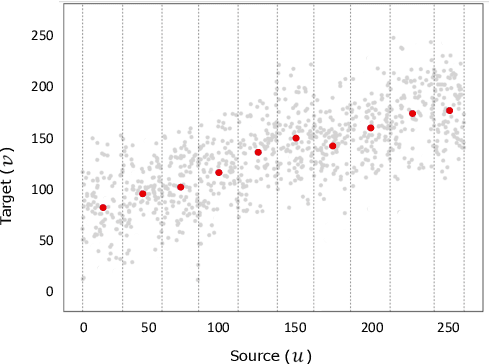
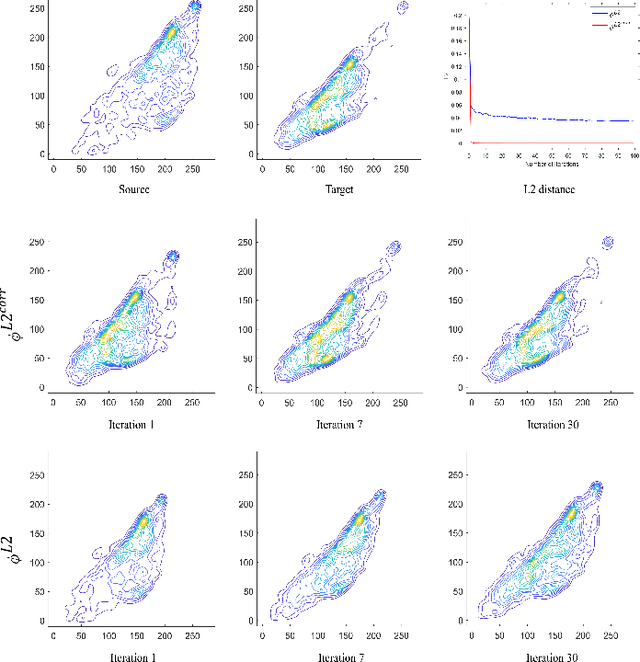
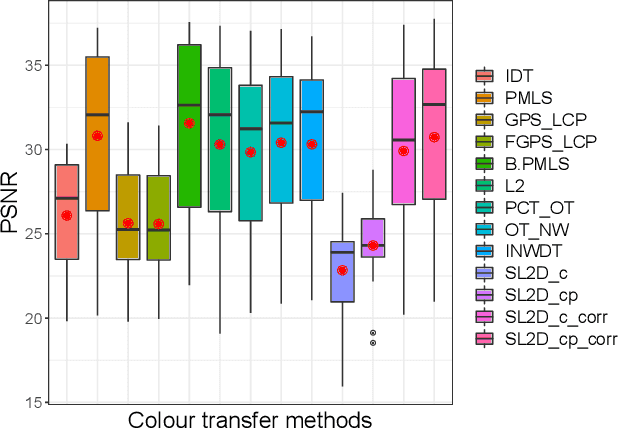
We propose a new method with $\mathcal{L}_2$ distance that maps one $N$-dimensional distribution to another, taking into account available information about correspondences. We solve the high-dimensional problem in 1D space using an iterative projection approach. To show the potentials of this mapping, we apply it to colour transfer between two images that exhibit overlapped scenes. Experiments show quantitative and qualitative competitive results as compared with the state of the art colour transfer methods.
* 5 pages, 9 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge