Hana Ćatić
Search-Based Task and Motion Planning for Hybrid Systems: Agile Autonomous Vehicles
Jan 25, 2023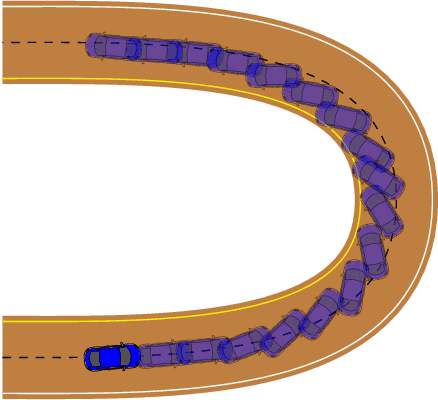
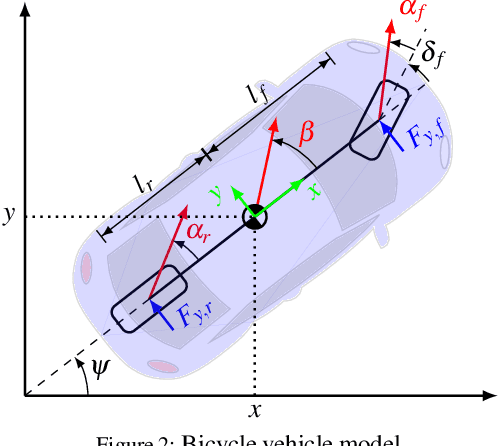
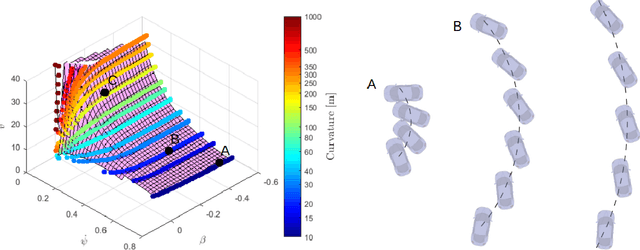
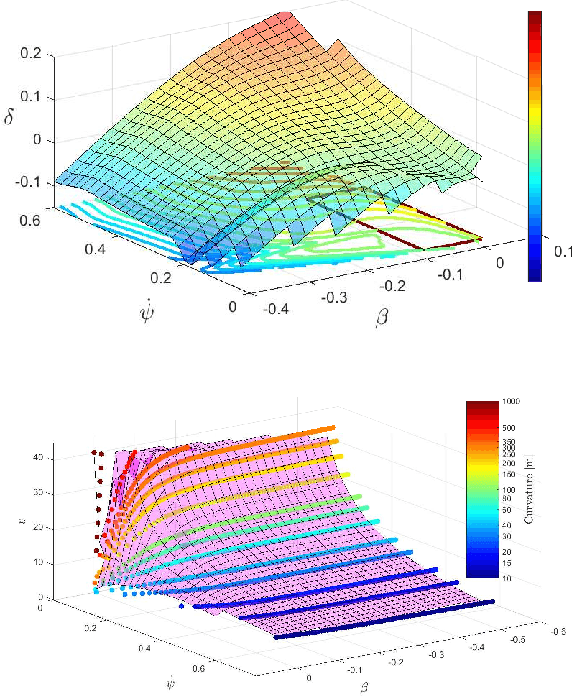
Abstract:To achieve optimal robot behavior in dynamic scenarios we need to consider complex dynamics in a predictive manner. In the vehicle dynamics community, it is well know that to achieve time-optimal driving on low surface, the vehicle should utilize drifting. Hence many authors have devised rules to split circuits and employ drifting on some segments. These rules are suboptimal and do not generalize to arbitrary circuit shapes (e.g., S-like curves). So, the question "When to go into which mode and how to drive in it?" remains unanswered. To choose the suitable mode (discrete decision), the algorithm needs information about the feasibility of the continuous motion in that mode. This makes it a class of Task and Motion Planning (TAMP) problems, which are known to be hard to solve optimally in real-time. In the AI planning community, search methods are commonly used. However, they cannot be directly applied to TAMP problems due to the continuous component. Here, we present a search-based method that effectively solves this problem and efficiently searches in a highly dimensional state space with nonlinear and unstable dynamics. The space of the possible trajectories is explored by sampling different combinations of motion primitives guided by the search. Our approach allows to use multiple locally approximated models to generate motion primitives (e.g., learned models of drifting) and effectively simplify the problem without losing accuracy. The algorithm performance is evaluated in simulated driving on a mixed-track with segments of different curvatures (right and left). Our code is available at https://git.io/JenvB
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge