Hierarchical Disentangled Representation for Invertible Image Denoising and Beyond

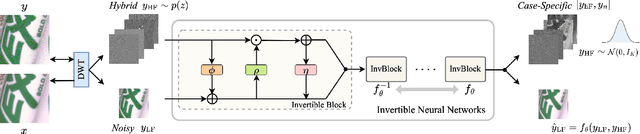
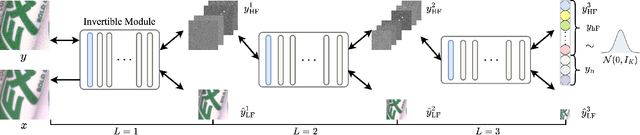
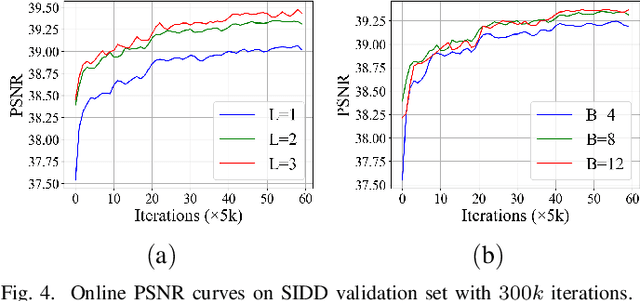
Image denoising is a typical ill-posed problem due to complex degradation. Leading methods based on normalizing flows have tried to solve this problem with an invertible transformation instead of a deterministic mapping. However, the implicit bijective mapping is not explored well. Inspired by a latent observation that noise tends to appear in the high-frequency part of the image, we propose a fully invertible denoising method that injects the idea of disentangled learning into a general invertible neural network to split noise from the high-frequency part. More specifically, we decompose the noisy image into clean low-frequency and hybrid high-frequency parts with an invertible transformation and then disentangle case-specific noise and high-frequency components in the latent space. In this way, denoising is made tractable by inversely merging noiseless low and high-frequency parts. Furthermore, we construct a flexible hierarchical disentangling framework, which aims to decompose most of the low-frequency image information while disentangling noise from the high-frequency part in a coarse-to-fine manner. Extensive experiments on real image denoising, JPEG compressed artifact removal, and medical low-dose CT image restoration have demonstrated that the proposed method achieves competing performance on both quantitative metrics and visual quality, with significantly less computational cost.

Looking at the posterior: on the origin of uncertainty in neural-network classification

Bayesian inference can quantify uncertainty in the predictions of neural networks using posterior distributions for model parameters and network output. By looking at these posterior distributions, one can separate the origin of uncertainty into aleatoric and epistemic. We use the joint distribution of predictive uncertainty and epistemic uncertainty to quantify how this interpretation of uncertainty depends upon model architecture, dataset complexity, and data distributional shifts in image classification tasks. We conclude that the origin of uncertainty is subjective to each neural network and that the quantification of the induced uncertainty from data distributional shifts depends on the complexity of the underlying dataset. Furthermore, we show that the joint distribution of predictive and epistemic uncertainty can be used to identify data domains where the model is most accurate. To arrive at these results, we use two common posterior approximation methods, Monte-Carlo dropout and deep ensembles, for fully-connected, convolutional and attention-based neural networks.