Finite-time Lyapunov exponents of deep neural networks

We compute how small input perturbations affect the output of deep neural networks, exploring an analogy between deep networks and dynamical systems, where the growth or decay of local perturbations is characterised by finite-time Lyapunov exponents. We show that the maximal exponent forms geometrical structures in input space, akin to coherent structures in dynamical systems. Ridges of large positive exponents divide input space into different regions that the network associates with different classes. These ridges visualise the geometry that deep networks construct in input space, shedding light on the fundamental mechanisms underlying their learning capabilities.

Looking at the posterior: on the origin of uncertainty in neural-network classification

Bayesian inference can quantify uncertainty in the predictions of neural networks using posterior distributions for model parameters and network output. By looking at these posterior distributions, one can separate the origin of uncertainty into aleatoric and epistemic. We use the joint distribution of predictive uncertainty and epistemic uncertainty to quantify how this interpretation of uncertainty depends upon model architecture, dataset complexity, and data distributional shifts in image classification tasks. We conclude that the origin of uncertainty is subjective to each neural network and that the quantification of the induced uncertainty from data distributional shifts depends on the complexity of the underlying dataset. Furthermore, we show that the joint distribution of predictive and epistemic uncertainty can be used to identify data domains where the model is most accurate. To arrive at these results, we use two common posterior approximation methods, Monte-Carlo dropout and deep ensembles, for fully-connected, convolutional and attention-based neural networks.

Constraints on parameter choices for successful reservoir computing

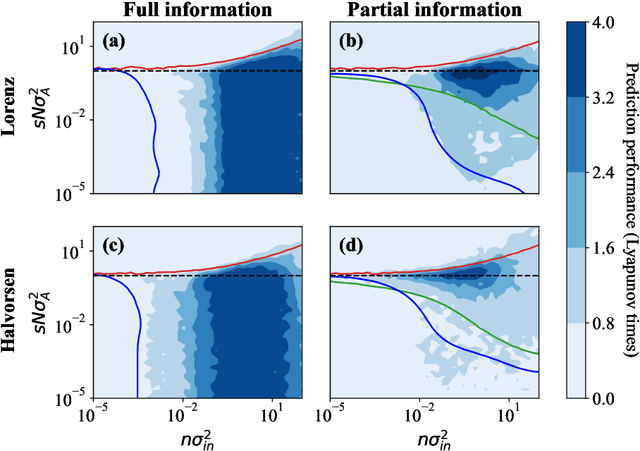
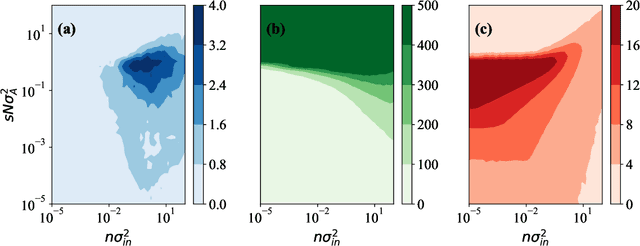
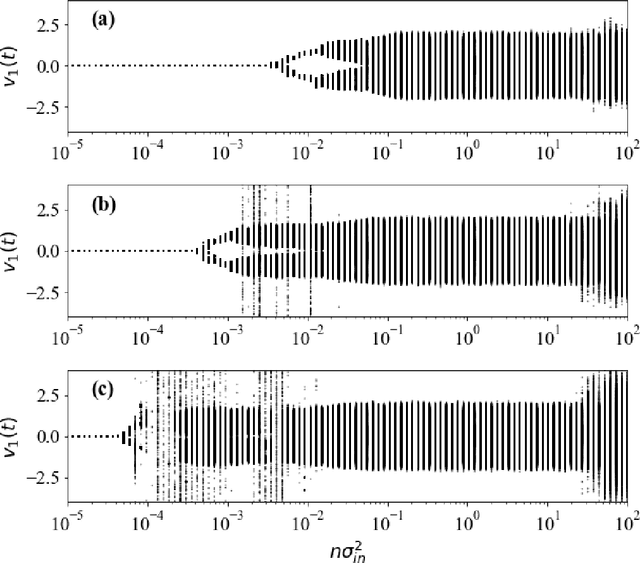
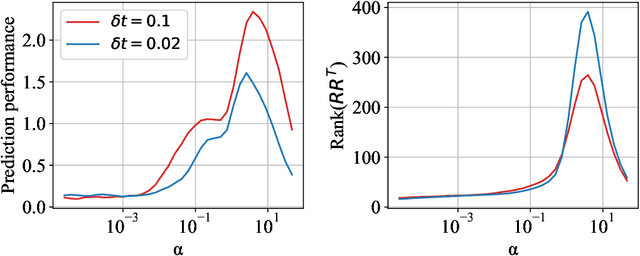
Echo-state networks are simple models of discrete dynamical systems driven by a time series. By selecting network parameters such that the dynamics of the network is contractive, characterized by a negative maximal Lyapunov exponent, the network may synchronize with the driving signal. Exploiting this synchronization, the echo-state network may be trained to autonomously reproduce the input dynamics, enabling time-series prediction. However, while synchronization is a necessary condition for prediction, it is not sufficient. Here, we study what other conditions are necessary for successful time-series prediction. We identify two key parameters for prediction performance, and conduct a parameter sweep to find regions where prediction is successful. These regions differ significantly depending on whether full or partial phase space information about the input is provided to the network during training. We explain how these regions emerge.

Improving traffic sign recognition by active search

We describe an iterative active-learning algorithm to recognise rare traffic signs. A standard ResNet is trained on a training set containing only a single sample of the rare class. We demonstrate that by sorting the samples of a large, unlabeled set by the estimated probability of belonging to the rare class, we can efficiently identify samples from the rare class. This works despite the fact that this estimated probability is usually quite low. A reliable active-learning loop is obtained by labeling these candidate samples, including them in the training set, and iterating the procedure. Further, we show that we get similar results starting from a single synthetic sample. Our results are important as they indicate a straightforward way of improving traffic-sign recognition for automated driving systems. In addition, they show that we can make use of the information hidden in low confidence outputs, which is usually ignored.

Artificial Neural Networks

These are lecture notes for my course on Artificial Neural Networks that I have given at Chalmers (FFR135) and Gothenburg University (FIM720). This course describes the use of neural networks in machine learning: deep learning, recurrent networks, and other supervised and unsupervised machine-learning algorithms.