Finite-time Lyapunov exponents of deep neural networks

We compute how small input perturbations affect the output of deep neural networks, exploring an analogy between deep networks and dynamical systems, where the growth or decay of local perturbations is characterised by finite-time Lyapunov exponents. We show that the maximal exponent forms geometrical structures in input space, akin to coherent structures in dynamical systems. Ridges of large positive exponents divide input space into different regions that the network associates with different classes. These ridges visualise the geometry that deep networks construct in input space, shedding light on the fundamental mechanisms underlying their learning capabilities.

Constraints on parameter choices for successful reservoir computing

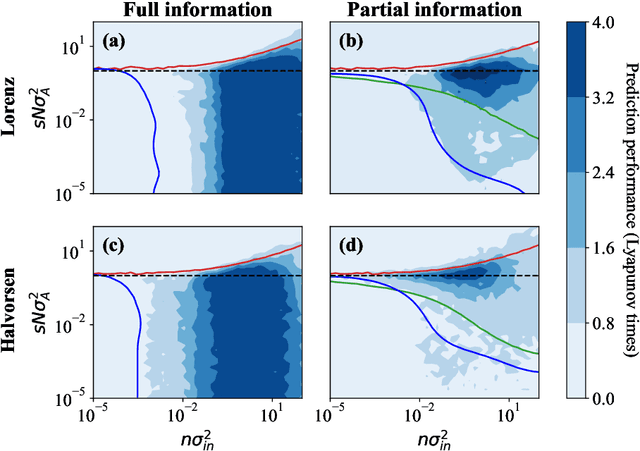
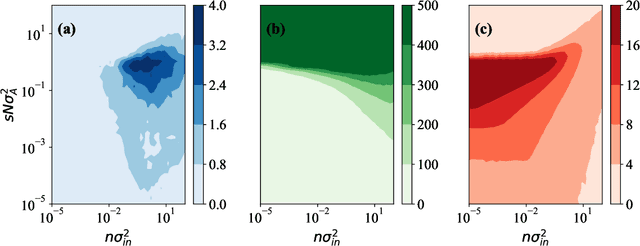
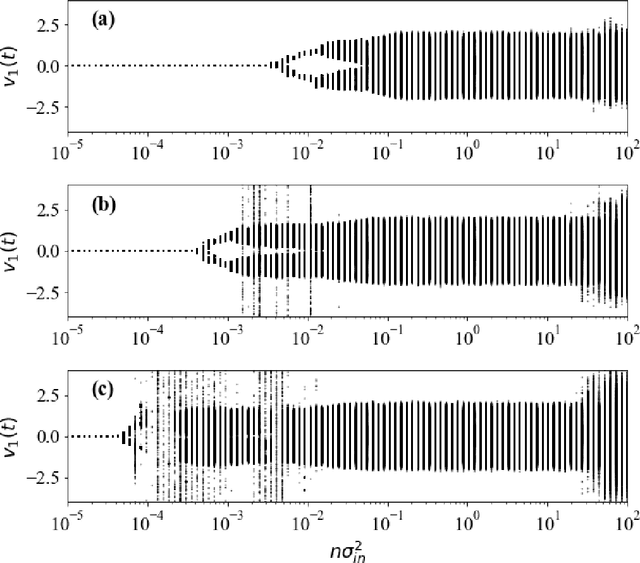
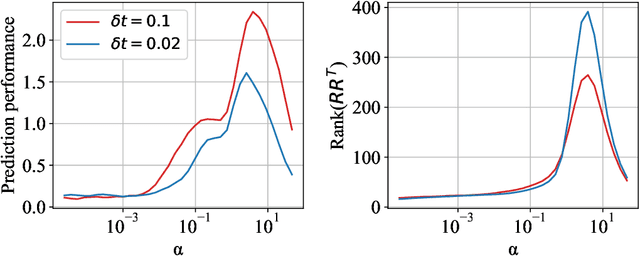
Echo-state networks are simple models of discrete dynamical systems driven by a time series. By selecting network parameters such that the dynamics of the network is contractive, characterized by a negative maximal Lyapunov exponent, the network may synchronize with the driving signal. Exploiting this synchronization, the echo-state network may be trained to autonomously reproduce the input dynamics, enabling time-series prediction. However, while synchronization is a necessary condition for prediction, it is not sufficient. Here, we study what other conditions are necessary for successful time-series prediction. We identify two key parameters for prediction performance, and conduct a parameter sweep to find regions where prediction is successful. These regions differ significantly depending on whether full or partial phase space information about the input is provided to the network during training. We explain how these regions emerge.