LARNN: Linear Attention Recurrent Neural Network

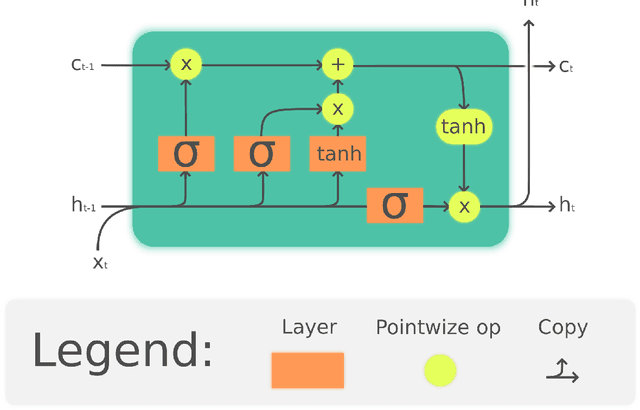
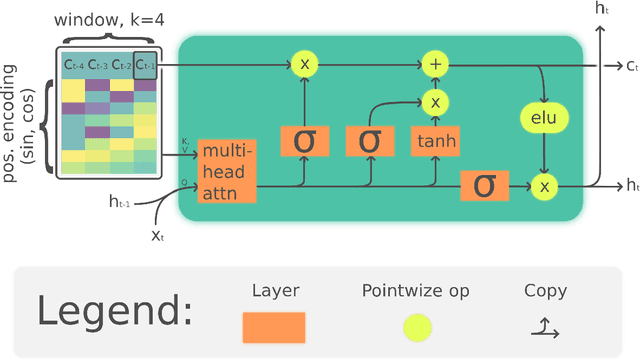
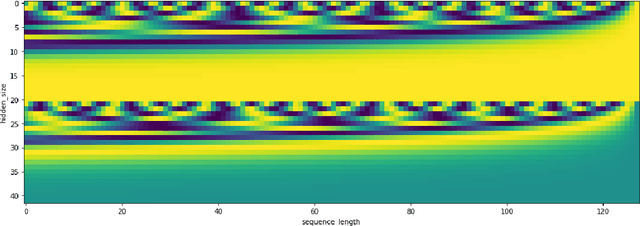
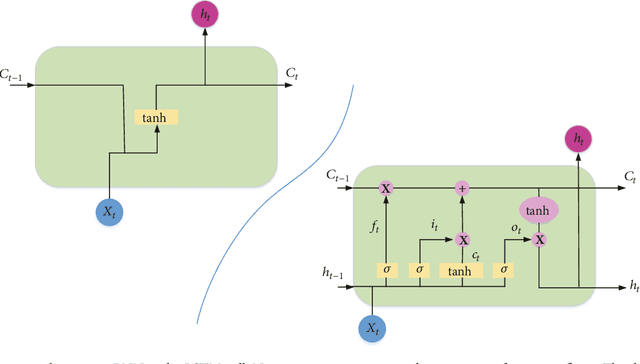
The Linear Attention Recurrent Neural Network (LARNN) is a recurrent attention module derived from the Long Short-Term Memory (LSTM) cell and ideas from the consciousness Recurrent Neural Network (RNN). Yes, it LARNNs. The LARNN uses attention on its past cell state values for a limited window size $k$. The formulas are also derived from the Batch Normalized LSTM (BN-LSTM) cell and the Transformer Network for its Multi-Head Attention Mechanism. The Multi-Head Attention Mechanism is used inside the cell such that it can query its own $k$ past values with the attention window. This has the effect of augmenting the rank of the tensor with the attention mechanism, such that the cell can perform complex queries to question its previous inner memories, which should augment the long short-term effect of the memory. With a clever trick, the LARNN cell with attention can be easily used inside a loop on the cell state, just like how any other Recurrent Neural Network (RNN) cell can be looped linearly through time series. This is due to the fact that its state, which is looped upon throughout time steps within time series, stores the inner states in a "first in, first out" queue which contains the $k$ most recent states and on which it is easily possible to add static positional encoding when the queue is represented as a tensor. This neural architecture yields better results than the vanilla LSTM cells. It can obtain results of 91.92% for the test accuracy, compared to the previously attained 91.65% using vanilla LSTM cells. Note that this is not to compare to other research, where up to 93.35% is obtained, but costly using 18 LSTM cells rather than with 2 to 3 cells as analyzed here. Finally, an interesting discovery is made, such that adding activation within the multi-head attention mechanism's linear layers can yield better results in the context researched hereto.

Deep Residual Bidir-LSTM for Human Activity Recognition Using Wearable Sensors

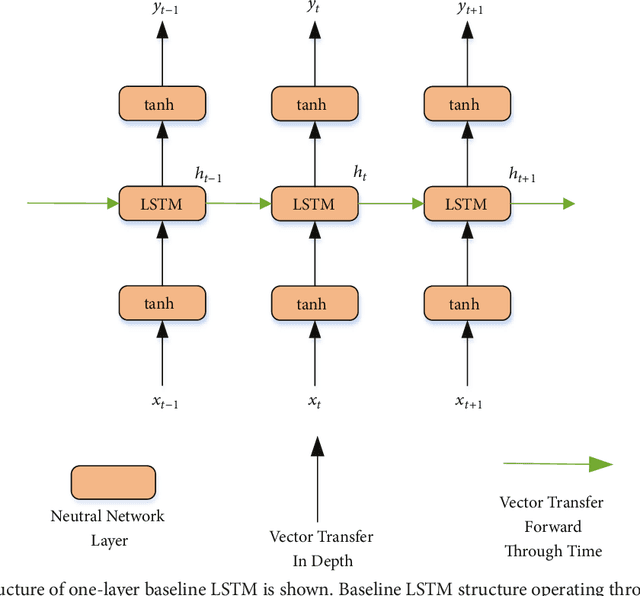
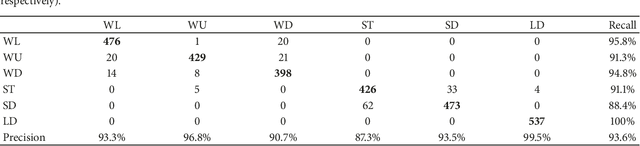
Human activity recognition (HAR) has become a popular topic in research because of its wide application. With the development of deep learning, new ideas have appeared to address HAR problems. Here, a deep network architecture using residual bidirectional long short-term memory (LSTM) cells is proposed. The advantages of the new network include that a bidirectional connection can concatenate the positive time direction (forward state) and the negative time direction (backward state). Second, residual connections between stacked cells act as highways for gradients, which can pass underlying information directly to the upper layer, effectively avoiding the gradient vanishing problem. Generally, the proposed network shows improvements on both the temporal (using bidirectional cells) and the spatial (residual connections stacked deeply) dimensions, aiming to enhance the recognition rate. When tested with the Opportunity data set and the public domain UCI data set, the accuracy was increased by 4.78% and 3.68%, respectively, compared with previously reported results. Finally, the confusion matrix of the public domain UCI data set was analyzed.

Applying Deep Bidirectional LSTM and Mixture Density Network for Basketball Trajectory Prediction

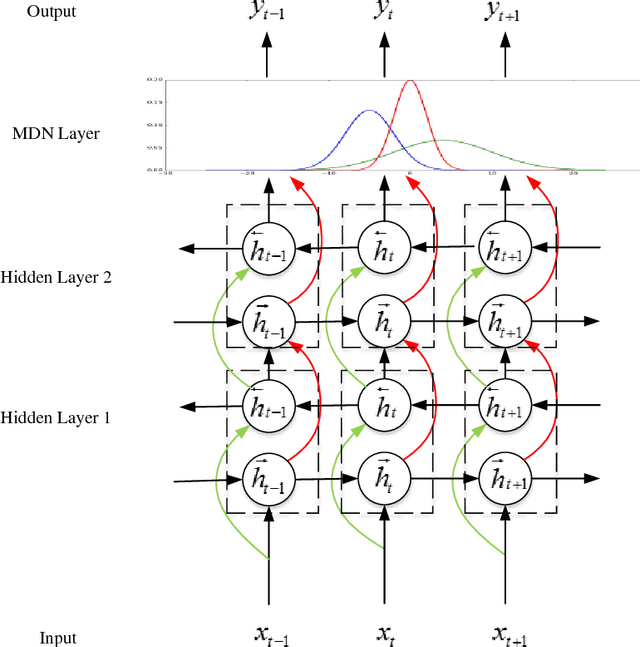
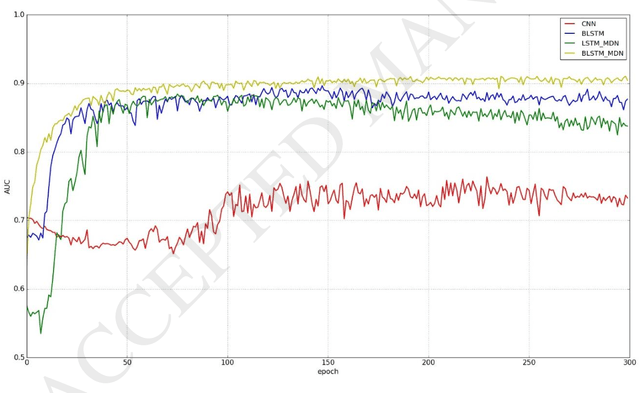
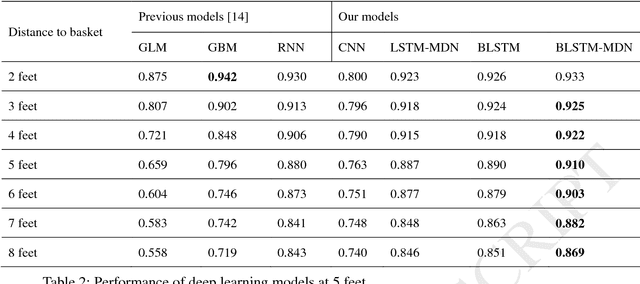
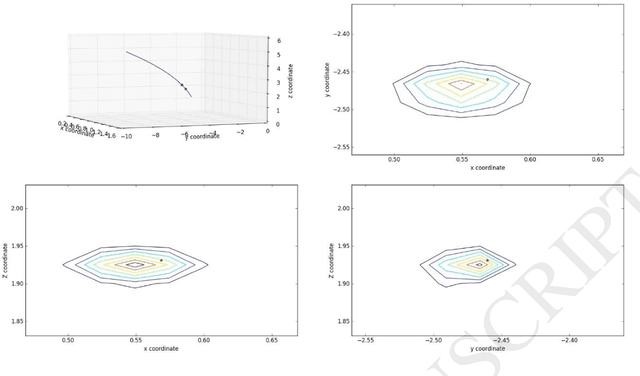
Data analytics helps basketball teams to create tactics. However, manual data collection and analytics are costly and ineffective. Therefore, we applied a deep bidirectional long short-term memory (BLSTM) and mixture density network (MDN) approach. This model is not only capable of predicting a basketball trajectory based on real data, but it also can generate new trajectory samples. It is an excellent application to help coaches and players decide when and where to shoot. Its structure is particularly suitable for dealing with time series problems. BLSTM receives forward and backward information at the same time, while stacking multiple BLSTMs further increases the learning ability of the model. Combined with BLSTMs, MDN is used to generate a multi-modal distribution of outputs. Thus, the proposed model can, in principle, represent arbitrary conditional probability distributions of output variables. We tested our model with two experiments on three-pointer datasets from NBA SportVu data. In the hit-or-miss classification experiment, the proposed model outperformed other models in terms of the convergence speed and accuracy. In the trajectory generation experiment, eight model-generated trajectories at a given time closely matched real trajectories.