On Multi-Stage Loss Dynamics in Neural Networks: Mechanisms of Plateau and Descent Stages

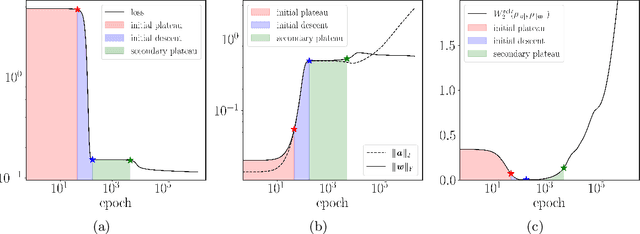
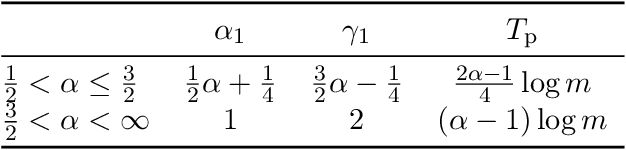
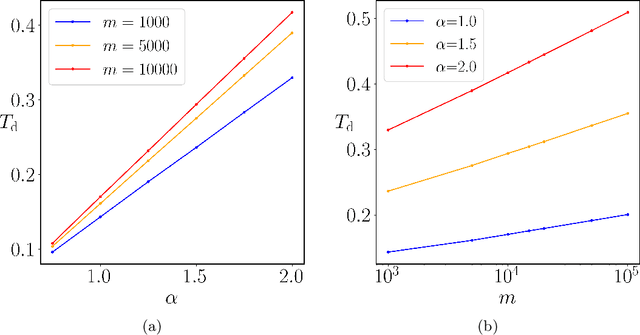
The multi-stage phenomenon in the training loss curves of neural networks has been widely observed, reflecting the non-linearity and complexity inherent in the training process. In this work, we investigate the training dynamics of neural networks (NNs), with particular emphasis on the small initialization regime, identifying three distinct stages observed in the loss curve during training: the initial plateau stage, the initial descent stage, and the secondary plateau stage. Through rigorous analysis, we reveal the underlying challenges contributing to slow training during the plateau stages. While the proof and estimate for the emergence of the initial plateau were established in our previous work, the behaviors of the initial descent and secondary plateau stages had not been explored before. Here, we provide a more detailed proof for the initial plateau, followed by a comprehensive analysis of the initial descent stage dynamics. Furthermore, we examine the factors facilitating the network's ability to overcome the prolonged secondary plateau, supported by both experimental evidence and heuristic reasoning. Finally, to clarify the link between global training trends and local parameter adjustments, we use the Wasserstein distance to track the fine-scale evolution of weight amplitude distribution.

Analyzing Multi-Stage Loss Curve: Plateau and Descent Mechanisms in Neural Networks

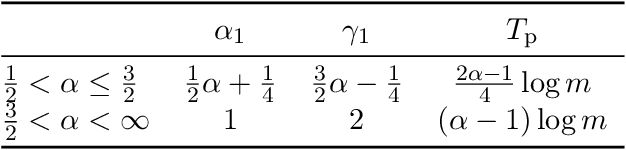
The multi-stage phenomenon in the training loss curves of neural networks has been widely observed, reflecting the non-linearity and complexity inherent in the training process. In this work, we investigate the training dynamics of neural networks (NNs), with particular emphasis on the small initialization regime and identify three distinct stages observed in the loss curve during training: initial plateau stage, initial descent stage, and secondary plateau stage. Through rigorous analysis, we reveal the underlying challenges causing slow training during the plateau stages. Building on existing work, we provide a more detailed proof for the initial plateau. This is followed by a comprehensive analysis of the dynamics in the descent stage. Furthermore, we explore the mechanisms that enable the network to overcome the prolonged secondary plateau stage, supported by both experimental evidence and heuristic reasoning. Finally, to better understand the relationship between global training trends and local parameter adjustments, we employ the Wasserstein distance to capture the microscopic evolution of weight amplitude distribution.