Guangxiao Yuan
Adaptive Divergence-based Non-negative Latent Factor Analysis
Mar 30, 2022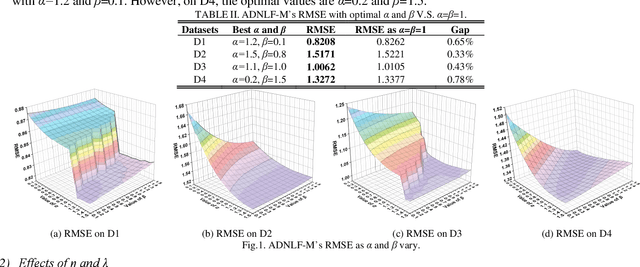
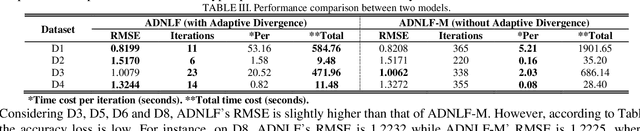
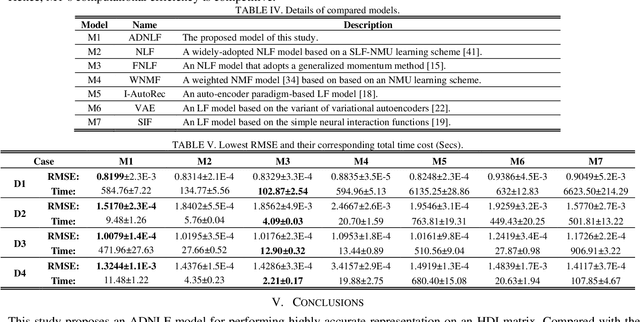
Abstract:High-Dimensional and Incomplete (HDI) data are frequently found in various industrial applications with complex interactions among numerous nodes, which are commonly non-negative for representing the inherent non-negativity of node interactions. A Non-negative Latent Factor (NLF) model is able to extract intrinsic features from such data efficiently. However, existing NLF models all adopt a static divergence metric like Euclidean distance or {\alpha}-\b{eta} divergence to build its learning objective, which greatly restricts its scalability of accurately representing HDI data from different domains. Aiming at addressing this issue, this study presents an Adaptive Divergence-based Non-negative Latent Factor (ADNLF) model with three-fold ideas: a) generalizing the objective function with the {\alpha}-\b{eta}-divergence to expand its potential of representing various HDI data; b) adopting a non-negative bridging function to connect the optimization variables with output latent factors for fulfilling the non-negativity constraints constantly; and c) making the divergence parameters adaptive through particle swarm optimization, thereby facilitating adaptive divergence in the learning objective to achieve high scalability. Empirical studies are conducted on four HDI datasets from real applications, whose results demonstrate that in comparison with state-of-the-art NLF models, an ADNLF model achieves significantly higher estimation accuracy for missing data of an HDI dataset with high computational efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge