Probabilistic Multi-Regional Solar Power Forecasting with Any-Quantile Recurrent Neural Networks

The increasing penetration of photovoltaic (PV) generation introduces significant uncertainty into power system operation, necessitating forecasting approaches that extend beyond deterministic point predictions. This paper proposes an any-quantile probabilistic forecasting framework for multi-regional PV power generation based on the Any-Quantile Recurrent Neural Network (AQ-RNN). The model integrates an any-quantile forecasting paradigm with a dual-track recurrent architecture that jointly processes series-specific and cross-regional contextual information, supported by dilated recurrent cells, patch-based temporal modeling, and a dynamic ensemble mechanism. The proposed framework enables the estimation of calibrated conditional quantiles at arbitrary probability levels within a single trained model and effectively exploits spatial dependencies to enhance robustness at the system level. The approach is evaluated using 30 years of hourly PV generation data from 259 European regions and compared against established statistical and neural probabilistic baselines. The results demonstrate consistent improvements in forecast accuracy, calibration, and prediction interval quality, underscoring the suitability of the proposed method for uncertainty-aware energy management and operational decision-making in renewable-dominated power systems.

Combining Forecasts using Meta-Learning: A Comparative Study for Complex Seasonality

In this paper, we investigate meta-learning for combining forecasts generated by models of different types. While typical approaches for combining forecasts involve simple averaging, machine learning techniques enable more sophisticated methods of combining through meta-learning, leading to improved forecasting accuracy. We use linear regression, $k$-nearest neighbors, multilayer perceptron, random forest, and long short-term memory as meta-learners. We define global and local meta-learning variants for time series with complex seasonality and compare meta-learners on multiple forecasting problems, demonstrating their superior performance compared to simple averaging.

Forecasting Cryptocurrency Prices using Contextual ES-adRNN with Exogenous Variables

In this paper, we introduce a new approach to multivariate forecasting cryptocurrency prices using a hybrid contextual model combining exponential smoothing (ES) and recurrent neural network (RNN). The model consists of two tracks: the context track and the main track. The context track provides additional information to the main track, extracted from representative series. This information as well as information extracted from exogenous variables is dynamically adjusted to the individual series forecasted by the main track. The RNN stacked architecture with hierarchical dilations, incorporating recently developed attentive dilated recurrent cells, allows the model to capture short and long-term dependencies across time series and dynamically weight input information. The model generates both point daily forecasts and predictive intervals for one-day, one-week and four-week horizons. We apply our model to forecast prices of 15 cryptocurrencies based on 17 input variables and compare its performance with that of comparative models, including both statistical and ML ones.

HKAN: Hierarchical Kolmogorov-Arnold Network without Backpropagation

This paper introduces the Hierarchical Kolmogorov-Arnold Network (HKAN), a novel network architecture that offers a competitive alternative to the recently proposed Kolmogorov-Arnold Network (KAN). Unlike KAN, which relies on backpropagation, HKAN adopts a randomized learning approach, where the parameters of its basis functions are fixed, and linear aggregations are optimized using least-squares regression. HKAN utilizes a hierarchical multi-stacking framework, with each layer refining the predictions from the previous one by solving a series of linear regression problems. This non-iterative training method simplifies computation and eliminates sensitivity to local minima in the loss function. Empirical results show that HKAN delivers comparable, if not superior, accuracy and stability relative to KAN across various regression tasks, while also providing insights into variable importance. The proposed approach seamlessly integrates theoretical insights with practical applications, presenting a robust and efficient alternative for neural network modeling.

Enhanced N-BEATS for Mid-Term Electricity Demand Forecasting

This paper presents an enhanced N-BEATS model, N-BEATS*, for improved mid-term electricity load forecasting (MTLF). Building on the strengths of the original N-BEATS architecture, which excels in handling complex time series data without requiring preprocessing or domain-specific knowledge, N-BEATS* introduces two key modifications. (1) A novel loss function -- combining pinball loss based on MAPE with normalized MSE, the new loss function allows for a more balanced approach by capturing both L1 and L2 loss terms. (2) A modified block architecture -- the internal structure of the N-BEATS blocks is adjusted by introducing a destandardization component to harmonize the processing of different time series, leading to more efficient and less complex forecasting tasks. Evaluated on real-world monthly electricity consumption data from 35 European countries, N-BEATS* demonstrates superior performance compared to its predecessor and other established forecasting methods, including statistical, machine learning, and hybrid models. N-BEATS* achieves the lowest MAPE and RMSE, while also exhibiting the lowest dispersion in forecast errors.

Stacking for Probabilistic Short-term Load Forecasting

In this study, we delve into the realm of meta-learning to combine point base forecasts for probabilistic short-term electricity demand forecasting. Our approach encompasses the utilization of quantile linear regression, quantile regression forest, and post-processing techniques involving residual simulation to generate quantile forecasts. Furthermore, we introduce both global and local variants of meta-learning. In the local-learning mode, the meta-model is trained using patterns most similar to the query pattern.Through extensive experimental studies across 35 forecasting scenarios and employing 16 base forecasting models, our findings underscored the superiority of quantile regression forest over its competitors

Any-Quantile Probabilistic Forecasting of Short-Term Electricity Demand

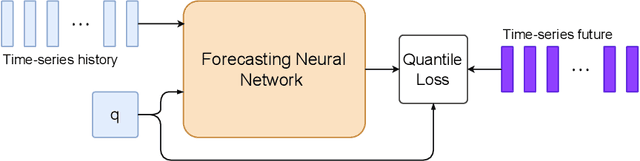
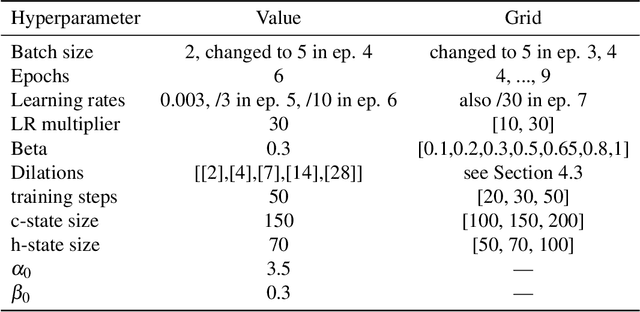
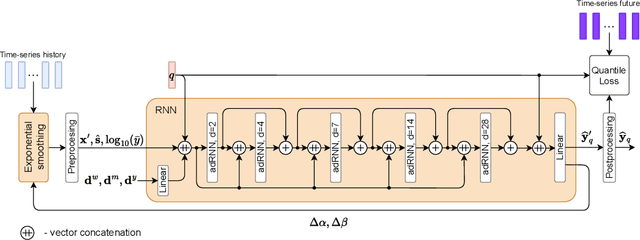
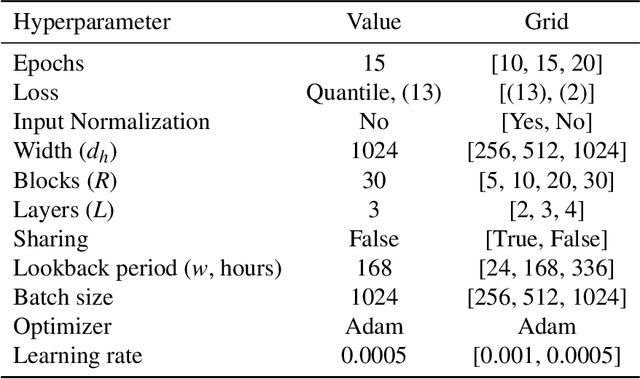
Power systems operate under uncertainty originating from multiple factors that are impossible to account for deterministically. Distributional forecasting is used to control and mitigate risks associated with this uncertainty. Recent progress in deep learning has helped to significantly improve the accuracy of point forecasts, while accurate distributional forecasting still presents a significant challenge. In this paper, we propose a novel general approach for distributional forecasting capable of predicting arbitrary quantiles. We show that our general approach can be seamlessly applied to two distinct neural architectures leading to the state-of-the-art distributional forecasting results in the context of short-term electricity demand forecasting task. We empirically validate our method on 35 hourly electricity demand time-series for European countries. Our code is available here: https://github.com/boreshkinai/any-quantile.

Contextually Enhanced ES-dRNN with Dynamic Attention for Short-Term Load Forecasting

In this paper, we propose a new short-term load forecasting (STLF) model based on contextually enhanced hybrid and hierarchical architecture combining exponential smoothing (ES) and a recurrent neural network (RNN). The model is composed of two simultaneously trained tracks: the context track and the main track. The context track introduces additional information to the main track. It is extracted from representative series and dynamically modulated to adjust to the individual series forecasted by the main track. The RNN architecture consists of multiple recurrent layers stacked with hierarchical dilations and equipped with recently proposed attentive dilated recurrent cells. These cells enable the model to capture short-term, long-term and seasonal dependencies across time series as well as to weight dynamically the input information. The model produces both point forecasts and predictive intervals. The experimental part of the work performed on 35 forecasting problems shows that the proposed model outperforms in terms of accuracy its predecessor as well as standard statistical models and state-of-the-art machine learning models.

STD: A Seasonal-Trend-Dispersion Decomposition of Time Series

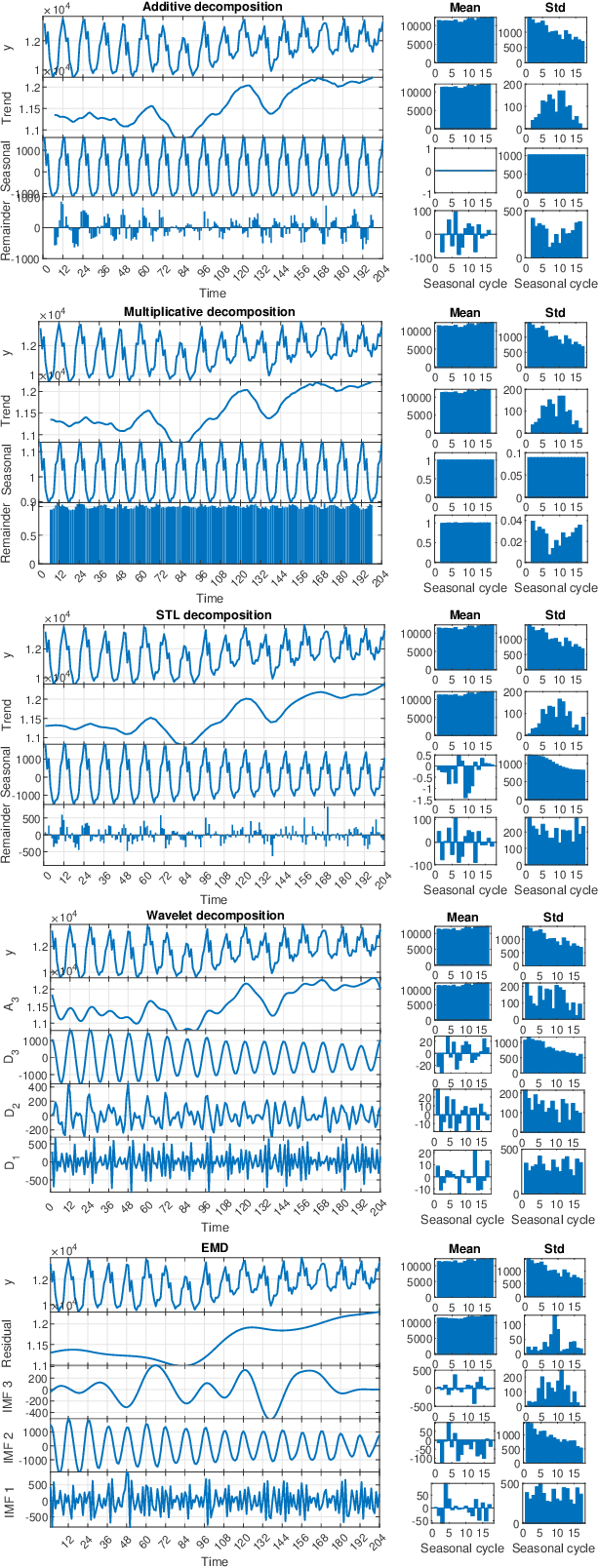
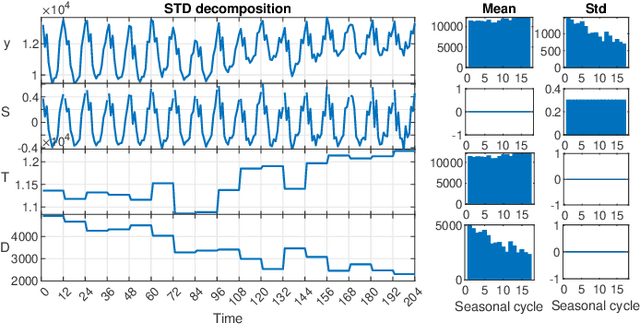
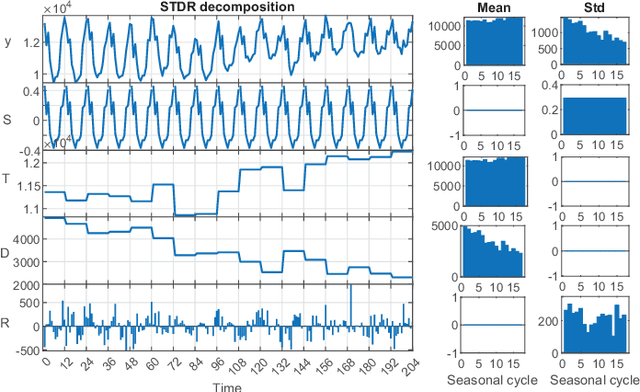
The decomposition of a time series is an essential task that helps to understand its very nature. It facilitates the analysis and forecasting of complex time series expressing various hidden components such as the trend, seasonal components, cyclic components and irregular fluctuations. Therefore, it is crucial in many fields for forecasting and decision processes. In recent years, many methods of time series decomposition have been developed, which extract and reveal different time series properties. Unfortunately, they neglect a very important property, i.e. time series variance. To deal with heteroscedasticity in time series, the method proposed in this work -- a seasonal-trend-dispersion decomposition (STD) -- extracts the trend, seasonal component and component related to the dispersion of the time series. We define STD decomposition in two ways: with and without an irregular component. We show how STD can be used for time series analysis and forecasting.

Recurrent Neural Networks for Forecasting Time Series with Multiple Seasonality: A Comparative Study

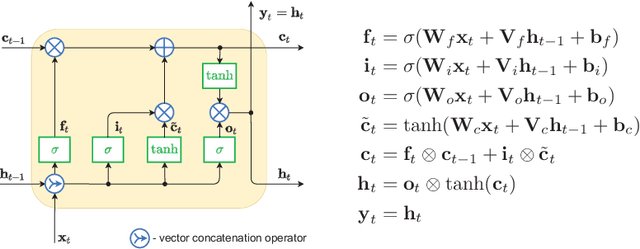
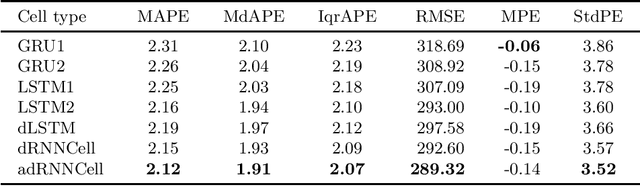
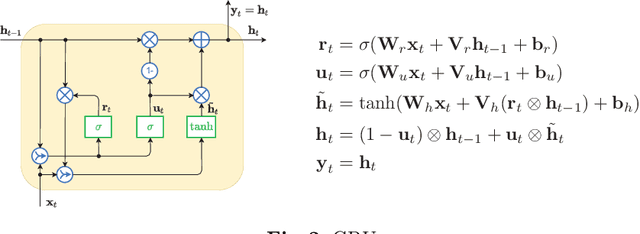
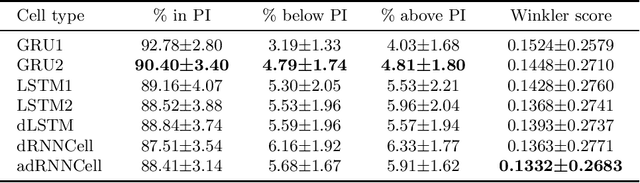
This paper compares recurrent neural networks (RNNs) with different types of gated cells for forecasting time series with multiple seasonality. The cells we compare include classical long short term memory (LSTM), gated recurrent unit (GRU), modified LSTM with dilation, and two new cells we proposed recently, which are equipped with dilation and attention mechanisms. To model the temporal dependencies of different scales, our RNN architecture has multiple dilated recurrent layers stacked with hierarchical dilations. The proposed RNN produces both point forecasts and predictive intervals (PIs) for them. An empirical study concerning short-term electrical load forecasting for 35 European countries confirmed that the new gated cells with dilation and attention performed best.