Predictive Covert Communication Against Multi-UAV Surveillance Using Graph Koopman Autoencoder

Low Probability of Detection (LPD) communication aims to obscure the presence of radio frequency (RF) signals to evade surveillance. In the context of mobile surveillance utilizing unmanned aerial vehicles (UAVs), achieving LPD communication presents significant challenges due to the UAVs' rapid and continuous movements, which are characterized by unknown nonlinear dynamics. Therefore, accurately predicting future locations of UAVs is essential for enabling real-time LPD communication. In this paper, we introduce a novel framework termed predictive covert communication, aimed at minimizing detectability in terrestrial ad-hoc networks under multi-UAV surveillance. Our data-driven method synergistically integrates graph neural networks (GNN) with Koopman theory to model the complex interactions within a multi-UAV network and facilitating long-term predictions by linearizing the dynamics, even with limited historical data. Extensive simulation results substantiate that the predicted trajectories using our method result in at least 63%-75% lower probability of detection when compared to well-known state-of-the-art baseline approaches, showing promise in enabling low-latency covert operations in practical scenarios.

Federated Graph Learning for Low Probability of Detection in Wireless Ad-Hoc Networks

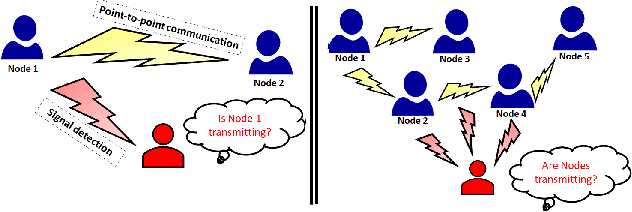
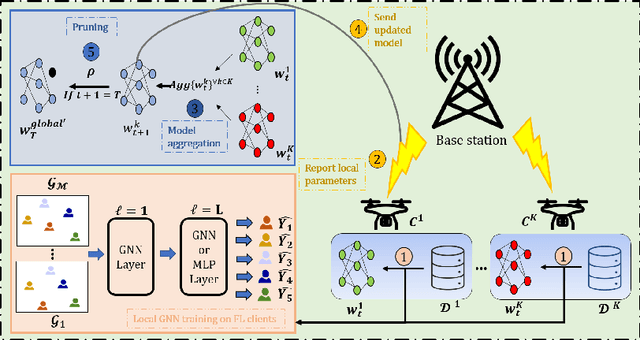
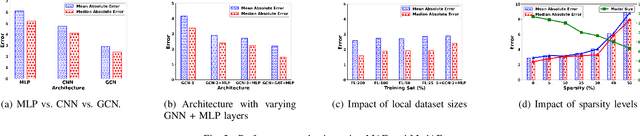
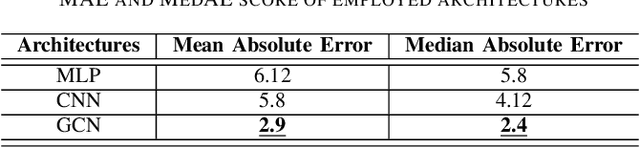
Low probability of detection (LPD) has recently emerged as a means to enhance the privacy and security of wireless networks. Unlike existing wireless security techniques, LPD measures aim to conceal the entire existence of wireless communication instead of safeguarding the information transmitted from users. Motivated by LPD communication, in this paper, we study a privacy-preserving and distributed framework based on graph neural networks to minimise the detectability of a wireless ad-hoc network as a whole and predict an optimal communication region for each node in the wireless network, allowing them to communicate while remaining undetected from external actors. We also demonstrate the effectiveness of the proposed method in terms of two performance measures, i.e., mean absolute error and median absolute error.