Learned Static Function Data Structures

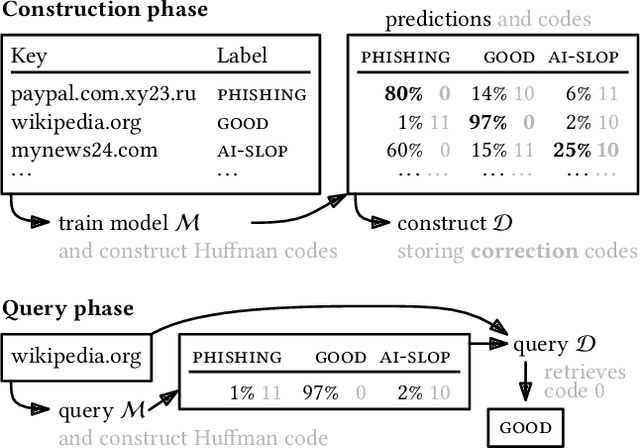
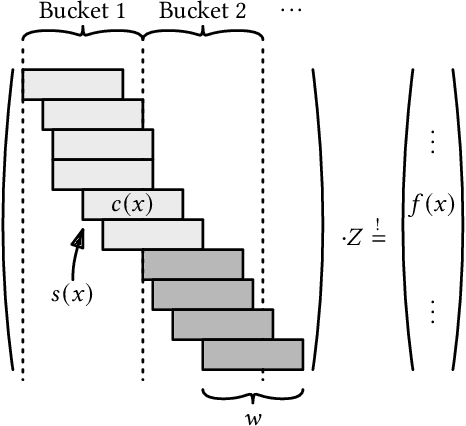
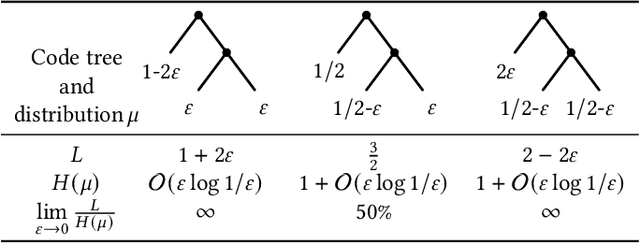
We consider the task of constructing a data structure for associating a static set of keys with values, while allowing arbitrary output values for queries involving keys outside the set. Compared to hash tables, these so-called static function data structures do not need to store the key set and thus use significantly less memory. Several techniques are known, with compressed static functions approaching the zero-order empirical entropy of the value sequence. In this paper, we introduce learned static functions, which use machine learning to capture correlations between keys and values. For each key, a model predicts a probability distribution over the values, from which we derive a key-specific prefix code to compactly encode the true value. The resulting codeword is stored in a classic static function data structure. This design allows learned static functions to break the zero-order entropy barrier while still supporting point queries. Our experiments show substantial space savings: up to one order of magnitude on real data, and up to three orders of magnitude on synthetic data.

Learned Compression of Nonlinear Time Series With Random Access

Time series play a crucial role in many fields, including finance, healthcare, industry, and environmental monitoring. The storage and retrieval of time series can be challenging due to their unstoppable growth. In fact, these applications often sacrifice precious historical data to make room for new data. General-purpose compressors can mitigate this problem with their good compression ratios, but they lack efficient random access on compressed data, thus preventing real-time analyses. Ad-hoc streaming solutions, instead, typically optimise only for compression and decompression speed, while giving up compression effectiveness and random access functionality. Furthermore, all these methods lack awareness of certain special regularities of time series, whose trends over time can often be described by some linear and nonlinear functions. To address these issues, we introduce NeaTS, a randomly-accessible compression scheme that approximates the time series with a sequence of nonlinear functions of different kinds and shapes, carefully selected and placed by a partitioning algorithm to minimise the space. The approximation residuals are bounded, which allows storing them in little space and thus recovering the original data losslessly, or simply discarding them to obtain a lossy time series representation with maximum error guarantees. Our experiments show that NeaTS improves the compression ratio of the state-of-the-art lossy compressors that use linear or nonlinear functions (or both) by up to 14%. Compared to lossless compressors, NeaTS emerges as the only approach to date providing, simultaneously, compression ratios close to or better than the best existing compressors, a much faster decompression speed, and orders of magnitude more efficient random access, thus enabling the storage and real-time analysis of massive and ever-growing amounts of (historical) time series data.

The PGM-index: a multicriteria, compressed and learned approach to data indexing

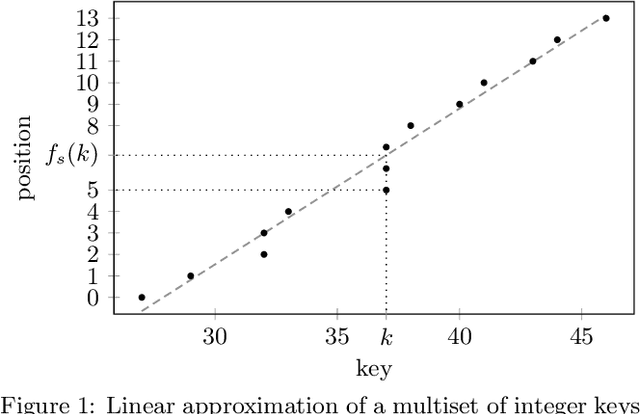
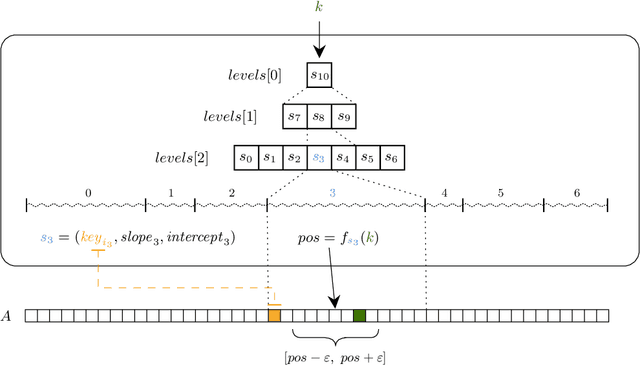
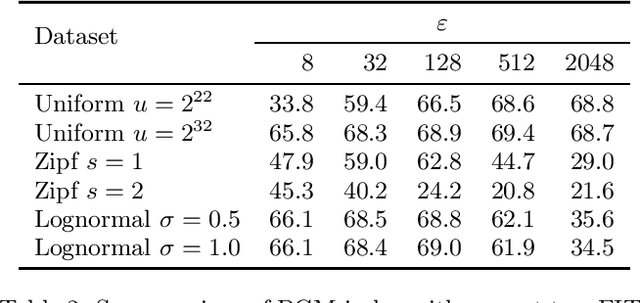
The recent introduction of learned indexes has shaken the foundations of the decades-old field of indexing data structures. Combining, or even replacing, classic design elements such as B-tree nodes with machine learning models has proven to give outstanding improvements in the space footprint and time efficiency of data systems. However, these novel approaches are based on heuristics, thus they lack any guarantees both in their time and space requirements. We propose the Piecewise Geometric Model index (shortly, PGM-index), which achieves guaranteed I/O-optimality in query operations, learns an optimal number of linear models, and its peculiar recursive construction makes it a purely learned data structure, rather than a hybrid of traditional and learned indexes (such as RMI and FITing-tree). We show that the PGM-index improves the space of the FITing-tree by 63.3% and of the B-tree by more than four orders of magnitude, while achieving their same or even better query time efficiency. We complement this result by proposing three variants of the PGM-index. First, we design a compressed PGM-index that further reduces its space footprint by exploiting the repetitiveness at the level of the learned linear models it is composed of. Second, we design a PGM-index that adapts itself to the distribution of the queries, thus resulting in the first known distribution-aware learned index to date. Finally, given its flexibility in the offered space-time trade-offs, we propose the multicriteria PGM-index that efficiently auto-tune itself in a few seconds over hundreds of millions of keys to the possibly evolving space-time constraints imposed by the application of use. We remark to the reader that this paper is an extended and improved version of our previous paper titled "Superseding traditional indexes by orchestrating learning and geometry" (arXiv:1903.00507).