Giorgio Parisi
The backtracking survey propagation algorithm for solving random K-SAT problems
Oct 06, 2016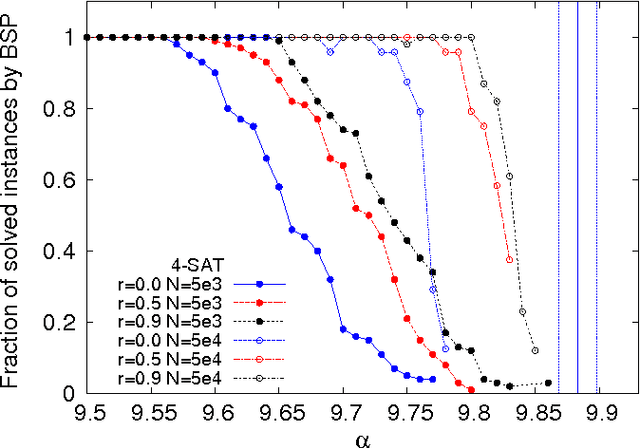
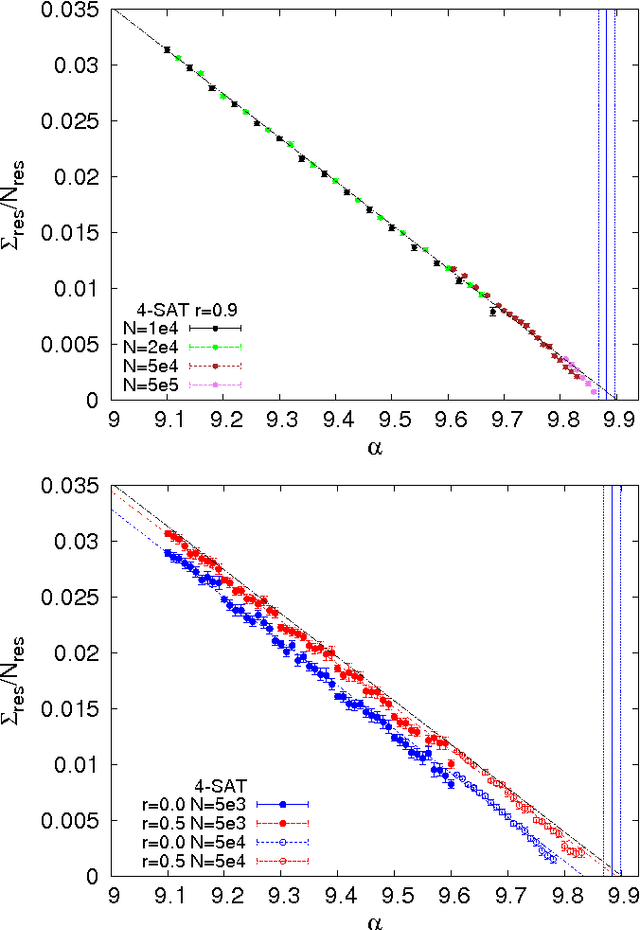
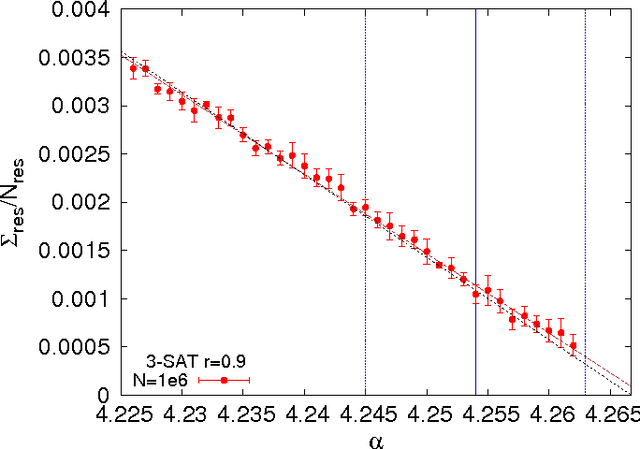
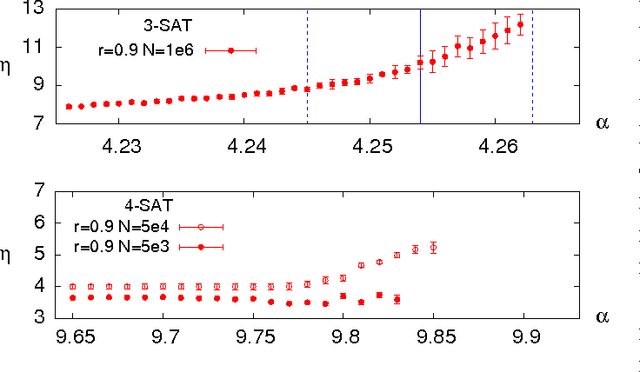
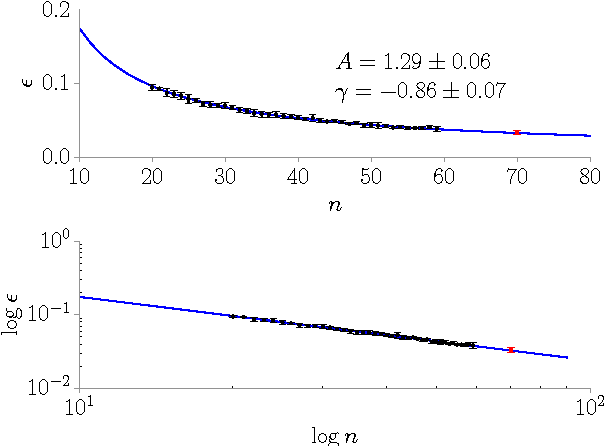
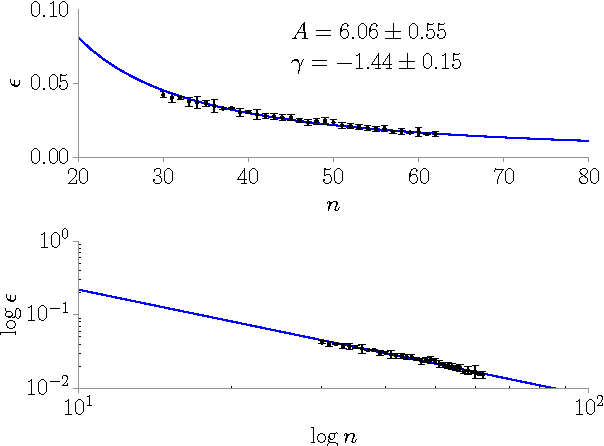
Abstract:Discrete combinatorial optimization has a central role in many scientific disciplines, however, for hard problems we lack linear time algorithms that would allow us to solve very large instances. Moreover, it is still unclear what are the key features that make a discrete combinatorial optimization problem hard to solve. Here we study random K-satisfiability problems with $K=3,4$, which are known to be very hard close to the SAT-UNSAT threshold, where problems stop having solutions. We show that the backtracking survey propagation algorithm, in a time practically linear in the problem size, is able to find solutions very close to the threshold, in a region unreachable by any other algorithm. All solutions found have no frozen variables, thus supporting the conjecture that only unfrozen solutions can be found in linear time, and that a problem becomes impossible to solve in linear time when all solutions contain frozen variables.
* 11 pages, 10 figures. v2: data largely improved and manuscript rewritten
Language discrimination and clustering via a neural network approach
Jul 15, 2015
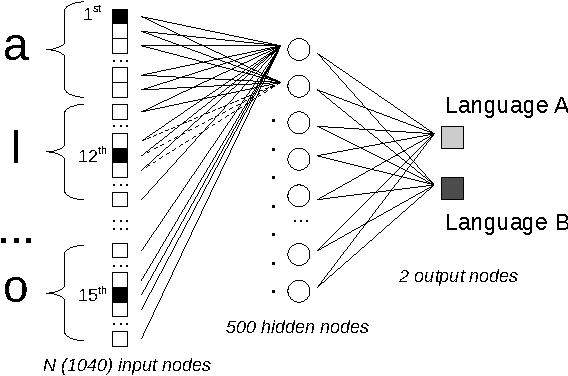
Abstract:We classify twenty-one Indo-European languages starting from written text. We use neural networks in order to define a distance among different languages, construct a dendrogram and analyze the ultrametric structure that emerges. Four or five subgroups of languages are identified, according to the "cut" of the dendrogram, drawn with an entropic criterion. The results and the method are discussed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge