Hierarchical Clustering and Matrix Completion for the Reconstruction of World Input-Output Tables

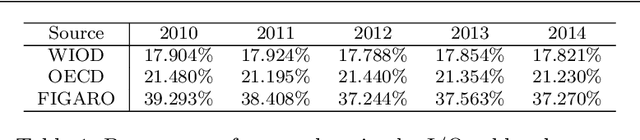
World Input-Output (I/O) matrices provide the networks of within- and cross-country economic relations. In the context of I/O analysis, the methodology adopted by national statistical offices in data collection raises the issue of obtaining reliable data in a timely fashion and it makes the reconstruction of (part of) the I/O matrices of particular interest. In this work, we propose a method combining hierarchical clustering and Matrix Completion (MC) with a LASSO-like nuclear norm penalty, to impute missing entries of a partially unknown I/O matrix. Through simulations based on synthetic matrices we study the effectiveness of the proposed method to predict missing values from both previous years data and current data related to countries similar to the one for which current data are obscured. To show the usefulness of our method, an application based on World Input-Output Database (WIOD) tables - which are an example of industry-by-industry I/O tables - is provided. Strong similarities in structure between WIOD and other I/O tables are also found, which make the proposed approach easily generalizable to them.

Principal Component Analysis Applied to Gradient Fields in Band Gap Optimization Problems for Metamaterials

A promising technique for the spectral design of acoustic metamaterials is based on the formulation of suitable constrained nonlinear optimization problems. Unfortunately, the straightforward application of classical gradient-based iterative optimization algorithms to the numerical solution of such problems is typically highly demanding, due to the complexity of the underlying physical models. Nevertheless, supervised machine learning techniques can reduce such a computational effort, e.g., by replacing the original objective functions of such optimization problems with more-easily computable approximations. In this framework, the present article describes the application of a related unsupervised machine learning technique, namely, principal component analysis, to approximate the gradient of the objective function of a band gap optimization problem for an acoustic metamaterial, with the aim of making the successive application of a gradient-based iterative optimization algorithm faster. Numerical results show the effectiveness of the proposed method.

On principal component analysis of the convex combination of two data matrices and its application to acoustic metamaterial filters

In this short paper, a matrix perturbation bound on the eigenvalues found by principal component analysis is investigated, for the case in which the data matrix on which principal component analysis is performed is a convex combination of two data matrices. The application of the theoretical analysis to multi-objective optimization problems (e.g., those arising in the design of acoustic metamaterial filters) is briefly discussed, together with possible extensions.

Machine-learning techniques for the optimal design of acoustic metamaterials

Recently, an increasing research effort has been dedicated to analyse the transmission and dispersion properties of periodic acoustic metamaterials, characterized by the presence of local resonators. Within this context, particular attention has been paid to the optimization of the amplitudes and center frequencies of selected stop and pass bands inside the Floquet-Bloch spectra of the acoustic metamaterials featured by a chiral or antichiral microstructure. Novel functional applications of such research are expected in the optimal parametric design of smart tunable mechanical filters and directional waveguides. The present paper deals with the maximization of the amplitude of low-frequency band gaps, by proposing suitable numerical techniques to solve the associated optimization problems. Specifically, the feasibility and effectiveness of Radial Basis Function networks and Quasi-Monte Carlo methods for the interpolation of the objective functions of such optimization problems are discussed, and their numerical application to a specific acoustic metamaterial with tetrachiral microstructure is presented. The discussion is motivated theoretically by the high computational effort often needed for an exact evaluation of the objective functions arising in band gap optimization problems, when iterative algorithms are used for their approximate solution. By replacing such functions with suitable surrogate objective functions constructed applying machine-learning techniques, well performing suboptimal solutions can be obtained with a smaller computational effort. Numerical results demonstrate the effective potential of the proposed approach. Current directions of research involving the use of additional machine-learning techniques are also presented.

Heterogeneous causal effects with imperfect compliance: a novel Bayesian machine learning approach

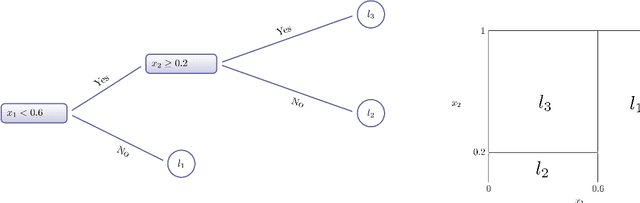
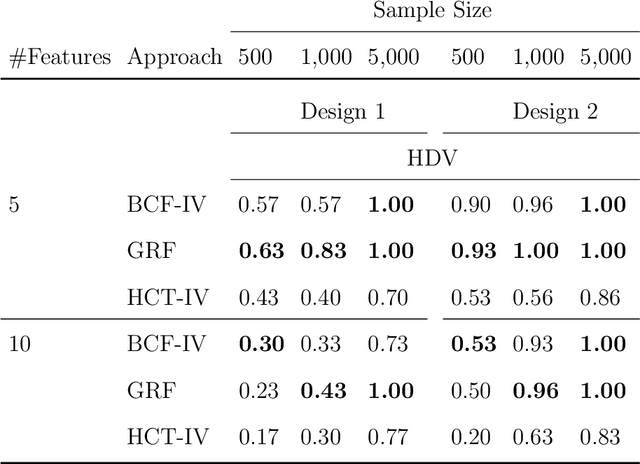
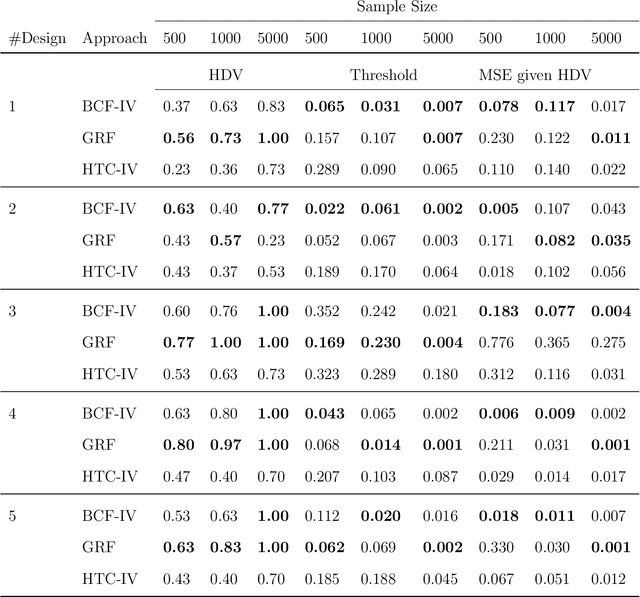
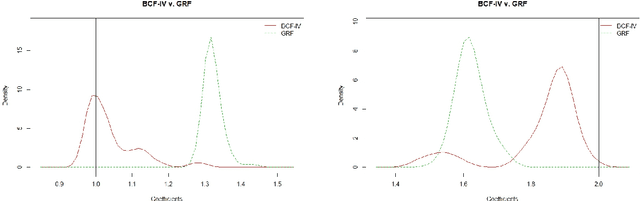
This paper introduces an innovative Bayesian machine learning algorithm to draw inference on heterogeneous causal effects in the presence of imperfect compliance (e.g., under an irregular assignment mechanism). We show, through Monte Carlo simulations, that the proposed Bayesian Causal Forest with Instrumental Variable (BCF-IV) algorithm outperforms other machine learning techniques tailored for causal inference (namely, Generalized Random Forest and Causal Trees with Instrumental Variable) in estimating the causal effects. Moreover, we show that it converges to an optimal asymptotic performance in discovering the drivers of heterogeneity in a simulated scenario. BCF-IV sheds a light on the heterogeneity of causal effects in instrumental variable scenarios and, in turn, provides the policy-makers with a relevant tool for targeted policies. Its empirical application evaluates the effects of additional funding on students' performances. The results indicate that BCF-IV could be used to enhance the effectiveness of school funding on students' performance by 3.2 to 3.5 times.

Estimating Heterogeneous Causal Effects in the Presence of Irregular Assignment Mechanisms

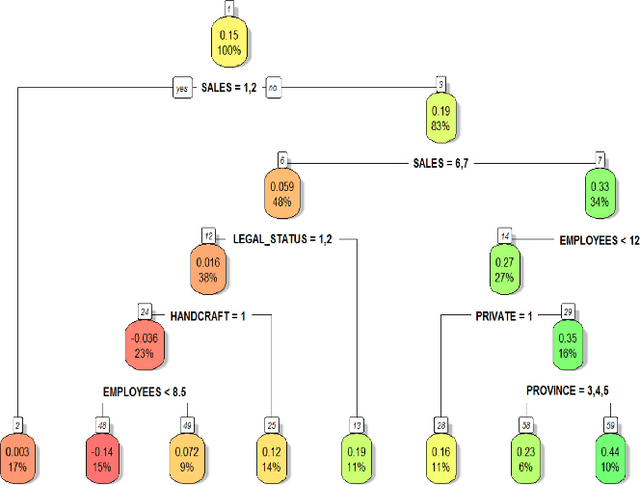
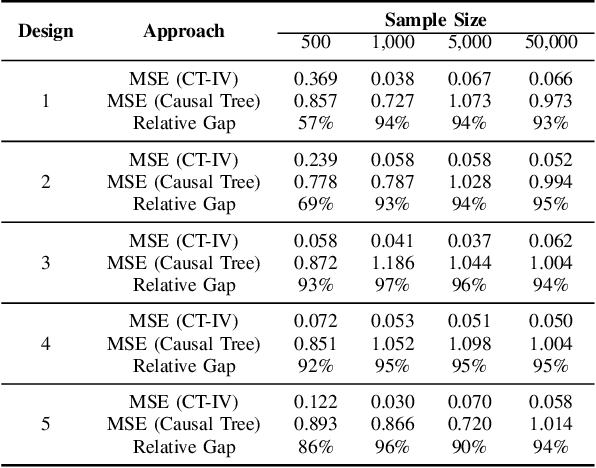
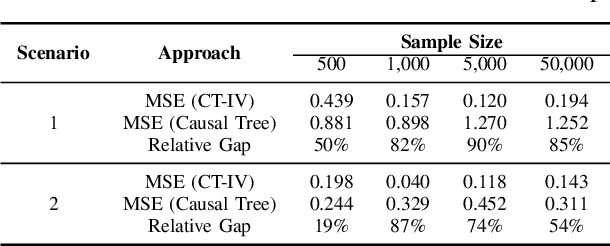
This paper provides a link between causal inference and machine learning techniques - specifically, Classification and Regression Trees (CART) - in observational studies where the receipt of the treatment is not randomized, but the assignment to the treatment can be assumed to be randomized (irregular assignment mechanism). The paper contributes to the growing applied machine learning literature on causal inference, by proposing a modified version of the Causal Tree (CT) algorithm to draw causal inference from an irregular assignment mechanism. The proposed method is developed by merging the CT approach with the instrumental variable framework to causal inference, hence the name Causal Tree with Instrumental Variable (CT-IV). As compared to CT, the main strength of CT-IV is that it can deal more efficiently with the heterogeneity of causal effects, as demonstrated by a series of numerical results obtained on synthetic data. Then, the proposed algorithm is used to evaluate a public policy implemented by the Tuscan Regional Administration (Italy), which aimed at easing the access to credit for small firms. In this context, CT-IV breaks fresh ground for target-based policies, identifying interesting heterogeneous causal effects.

Symmetric and antisymmetric properties of solutions to kernel-based machine learning problems

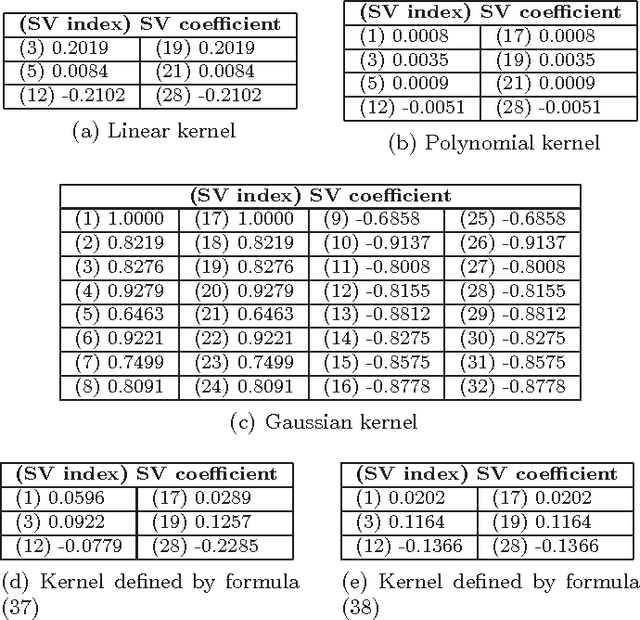
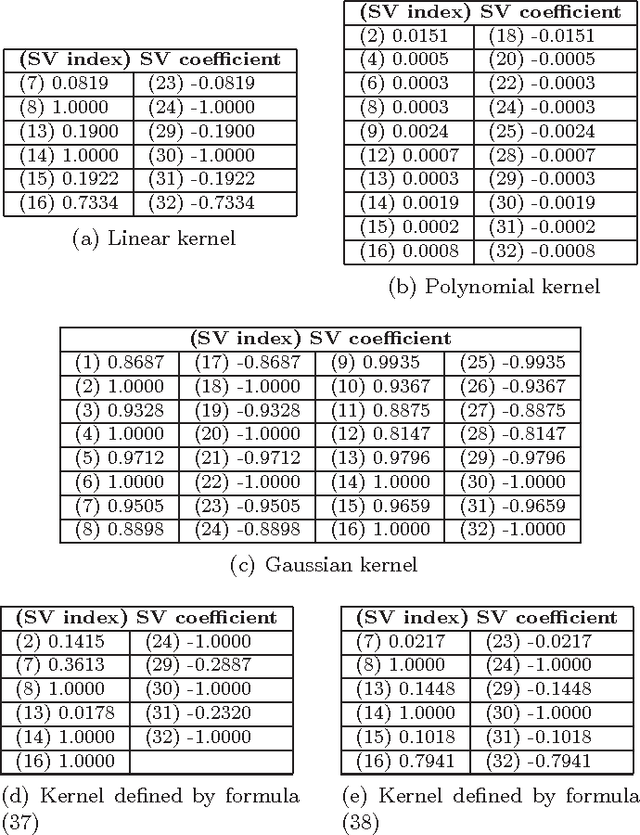
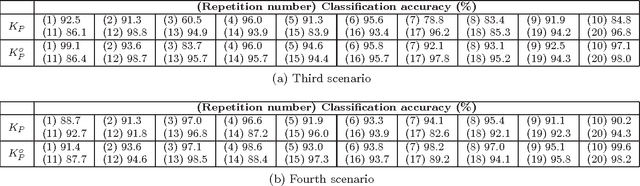
A particularly interesting instance of supervised learning with kernels is when each training example is associated with two objects, as in pairwise classification (Brunner et al., 2012), and in supervised learning of preference relations (Herbrich et al., 1998). In these cases, one may want to embed additional prior knowledge into the optimization problem associated with the training of the learning machine, modeled, respectively, by the symmetry of its optimal solution with respect to an exchange of order between the two objects, and by its antisymmetry. Extending the approach proposed in (Brunner et al., 2012) (where the only symmetric case was considered), we show, focusing on support vector binary classification, how such embedding is possible through the choice of a suitable pairwise kernel, which takes as inputs the individual feature vectors and also the group feature vectors associated with the two objects. We also prove that the symmetry/antisymmetry constraints still hold when considering the sequence of suboptimal solutions generated by one version of the Sequential Minimal Optimization (SMO) algorithm, and we present numerical results supporting the theoretical findings. We conclude discussing extensions of the main results to support vector regression, to transductive support vector machines, and to several kinds of graph kernels, including diffusion kernels.