Symmetric and antisymmetric properties of solutions to kernel-based machine learning problems
Paper and Code
Oct 28, 2016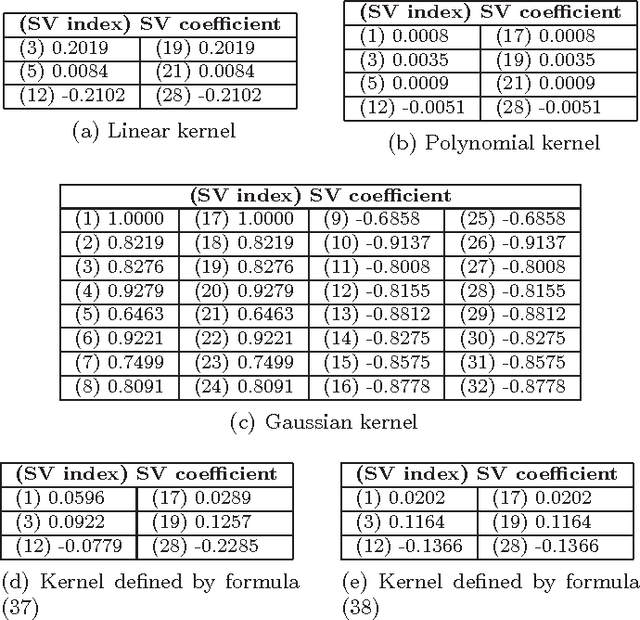
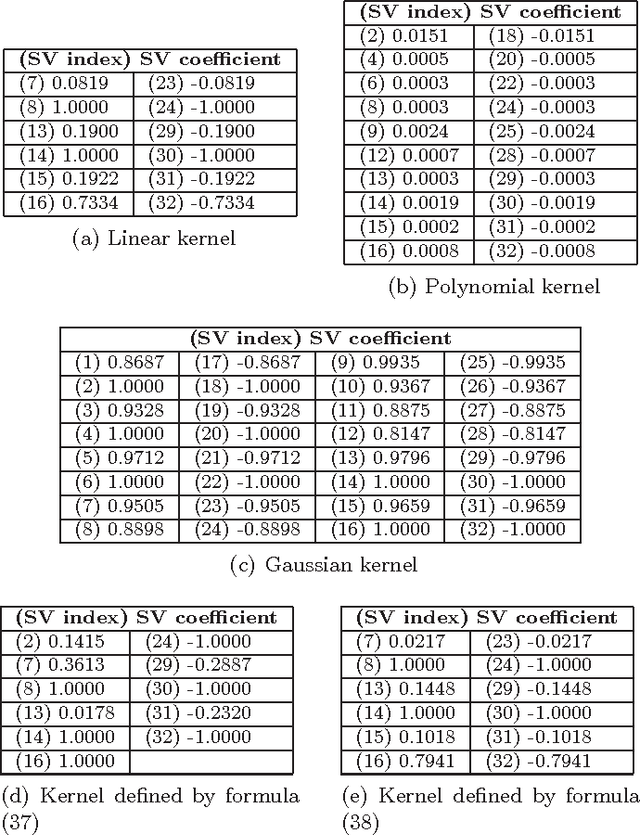
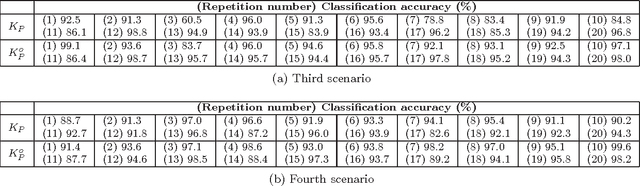
A particularly interesting instance of supervised learning with kernels is when each training example is associated with two objects, as in pairwise classification (Brunner et al., 2012), and in supervised learning of preference relations (Herbrich et al., 1998). In these cases, one may want to embed additional prior knowledge into the optimization problem associated with the training of the learning machine, modeled, respectively, by the symmetry of its optimal solution with respect to an exchange of order between the two objects, and by its antisymmetry. Extending the approach proposed in (Brunner et al., 2012) (where the only symmetric case was considered), we show, focusing on support vector binary classification, how such embedding is possible through the choice of a suitable pairwise kernel, which takes as inputs the individual feature vectors and also the group feature vectors associated with the two objects. We also prove that the symmetry/antisymmetry constraints still hold when considering the sequence of suboptimal solutions generated by one version of the Sequential Minimal Optimization (SMO) algorithm, and we present numerical results supporting the theoretical findings. We conclude discussing extensions of the main results to support vector regression, to transductive support vector machines, and to several kinds of graph kernels, including diffusion kernels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge