3D Roadway Scene Object Detection with LIDARs in Snowfall Conditions

Because 3D structure of a roadway environment can be characterized directly by a Light Detection and Ranging (LiDAR) sensors, they can be used to obtain exceptional situational awareness for assitive and autonomous driving systems. Although LiDARs demonstrate good performance in clean and clear weather conditions, their performance significantly deteriorates in adverse weather conditions such as those involving atmospheric precipitation. This may render perception capabilities of autonomous systems that use LiDAR data in learning based models to perform object detection and ranging ineffective. While efforts have been made to enhance the accuracy of these models, the extent of signal degradation under various weather conditions remains largely not quantified. In this study, we focus on the performance of an automotive grade LiDAR in snowy conditions in order to develop a physics-based model that examines failure modes of a LiDAR sensor. Specifically, we investigated how the LiDAR signal attenuates with different snowfall rates and how snow particles near the source serve as small but efficient reflectors. Utilizing our model, we transform data from clear conditions to simulate snowy scenarios, enabling a comparison of our synthetic data with actual snowy conditions. Furthermore, we employ this synthetic data, representative of different snowfall rates, to explore the impact on a pre-trained object detection model, assessing its performance under varying levels of snowfall

Deep Learning-Based Analysis of Power Consumption in Gasoline, Electric, and Hybrid Vehicles

Accurate power consumption prediction is crucial for improving efficiency and reducing environmental impact, yet traditional methods relying on specialized instruments or rigid physical models are impractical for large-scale, real-world deployment. This study introduces a scalable data-driven method using powertrain dynamic feature sets and both traditional machine learning and deep neural networks to estimate instantaneous and cumulative power consumption in internal combustion engine (ICE), electric vehicle (EV), and hybrid electric vehicle (HEV) platforms. ICE models achieved high instantaneous accuracy with mean absolute error and root mean squared error on the order of $10^{-3}$, and cumulative errors under 3%. Transformer and long short-term memory models performed best for EVs and HEVs, with cumulative errors below 4.1% and 2.1%, respectively. Results confirm the approach's effectiveness across vehicles and models. Uncertainty analysis revealed greater variability in EV and HEV datasets than ICE, due to complex power management, emphasizing the need for robust models for advanced powertrains.

Physics-Informed Neural Networks: Minimizing Residual Loss with Wide Networks and Effective Activations

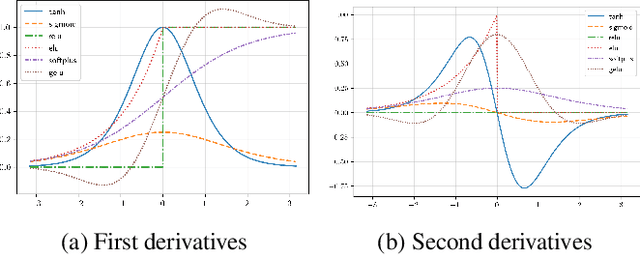
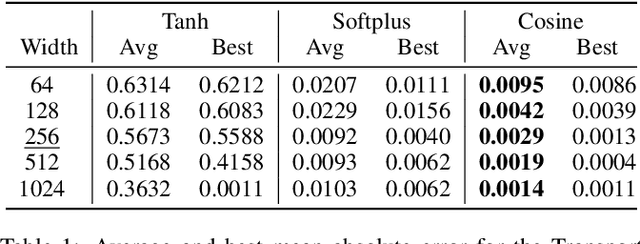
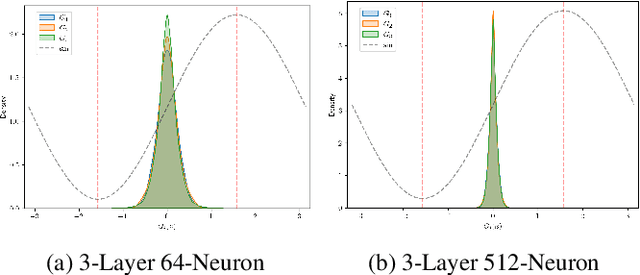
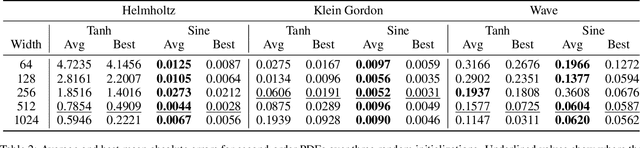
The residual loss in Physics-Informed Neural Networks (PINNs) alters the simple recursive relation of layers in a feed-forward neural network by applying a differential operator, resulting in a loss landscape that is inherently different from those of common supervised problems. Therefore, relying on the existing theory leads to unjustified design choices and suboptimal performance. In this work, we analyze the residual loss by studying its characteristics at critical points to find the conditions that result in effective training of PINNs. Specifically, we first show that under certain conditions, the residual loss of PINNs can be globally minimized by a wide neural network. Furthermore, our analysis also reveals that an activation function with well-behaved high-order derivatives plays a crucial role in minimizing the residual loss. In particular, to solve a $k$-th order PDE, the $k$-th derivative of the activation function should be bijective. The established theory paves the way for designing and choosing effective activation functions for PINNs and explains why periodic activations have shown promising performance in certain cases. Finally, we verify our findings by conducting a set of experiments on several PDEs. Our code is publicly available at https://github.com/nimahsn/pinns_tf2.

Momentum Diminishes the Effect of Spectral Bias in Physics-Informed Neural Networks

Physics-informed neural network (PINN) algorithms have shown promising results in solving a wide range of problems involving partial differential equations (PDEs). However, they often fail to converge to desirable solutions when the target function contains high-frequency features, due to a phenomenon known as spectral bias. In the present work, we exploit neural tangent kernels (NTKs) to investigate the training dynamics of PINNs evolving under stochastic gradient descent with momentum (SGDM). This demonstrates SGDM significantly reduces the effect of spectral bias. We have also examined why training a model via the Adam optimizer can accelerate the convergence while reducing the spectral bias. Moreover, our numerical experiments have confirmed that wide-enough networks using SGDM still converge to desirable solutions, even in the presence of high-frequency features. In fact, we show that the width of a network plays a critical role in convergence.