Practical Aspects on Solving Differential Equations Using Deep Learning: A Primer

Deep learning has become a popular tool across many scientific fields, including the study of differential equations, particularly partial differential equations. This work introduces the basic principles of deep learning and the Deep Galerkin method, which uses deep neural networks to solve differential equations. This primer aims to provide technical and practical insights into the Deep Galerkin method and its implementation. We demonstrate how to solve the one-dimensional heat equation step-by-step. We also show how to apply the Deep Galerkin method to solve systems of ordinary differential equations and integral equations, such as the Fredholm of the second kind. Additionally, we provide code snippets within the text and the complete source code on Github. The examples are designed so that one can run them on a simple computer without needing a GPU.

Randomized Self Organizing Map

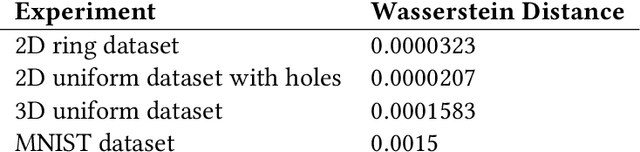
We propose a variation of the self organizing map algorithm by considering the random placement of neurons on a two-dimensional manifold, following a blue noise distribution from which various topologies can be derived. These topologies possess random (but controllable) discontinuities that allow for a more flexible self-organization, especially with high-dimensional data. The proposed algorithm is tested on one-, two- and three-dimensions tasks as well as on the MNIST handwritten digits dataset and validated using spectral analysis and topological data analysis tools. We also demonstrate the ability of the randomized self-organizing map to gracefully reorganize itself in case of neural lesion and/or neurogenesis.