Georgios Iosifidis
Optimistic No-regret Algorithms for Discrete Caching
Aug 15, 2022
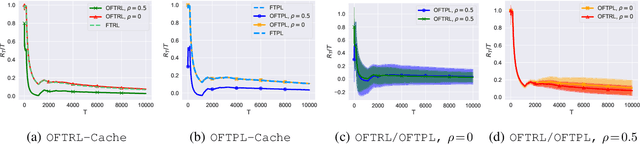


Abstract:We take a systematic look at the problem of storing whole files in a cache with limited capacity in the context of optimistic learning, where the caching policy has access to a prediction oracle (provided by, e.g., a Neural Network). The successive file requests are assumed to be generated by an adversary, and no assumption is made on the accuracy of the oracle. In this setting, we provide a universal lower bound for prediction-assisted online caching and proceed to design a suite of policies with a range of performance-complexity trade-offs. All proposed policies offer sublinear regret bounds commensurate with the accuracy of the oracle. Our results substantially improve upon all recently-proposed online caching policies, which, being unable to exploit the oracle predictions, offer only $O(\sqrt{T})$ regret. In this pursuit, we design, to the best of our knowledge, the first comprehensive optimistic Follow-the-Perturbed leader policy, which generalizes beyond the caching problem. We also study the problem of caching files with different sizes and the bipartite network caching problem. Finally, we evaluate the efficacy of the proposed policies through extensive numerical experiments using real-world traces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge