What Neuroscience Can Teach AI About Learning in Continuously Changing Environments

Modern AI models, such as large language models, are usually trained once on a huge corpus of data, potentially fine-tuned for a specific task, and then deployed with fixed parameters. Their training is costly, slow, and gradual, requiring billions of repetitions. In stark contrast, animals continuously adapt to the ever-changing contingencies in their environments. This is particularly important for social species, where behavioral policies and reward outcomes may frequently change in interaction with peers. The underlying computational processes are often marked by rapid shifts in an animal's behaviour and rather sudden transitions in neuronal population activity. Such computational capacities are of growing importance for AI systems operating in the real world, like those guiding robots or autonomous vehicles, or for agentic AI interacting with humans online. Can AI learn from neuroscience? This Perspective explores this question, integrating the literature on continual and in-context learning in AI with the neuroscience of learning on behavioral tasks with shifting rules, reward probabilities, or outcomes. We will outline an agenda for how specifically insights from neuroscience may inform current developments in AI in this area, and - vice versa - what neuroscience may learn from AI, contributing to the evolving field of NeuroAI.

Uncovering the Functional Roles of Nonlinearity in Memory

Memory and long-range temporal processing are core requirements for sequence modeling tasks across natural language processing, time-series forecasting, speech recognition, and control. While nonlinear recurrence has long been viewed as essential for enabling such mechanisms, recent work suggests that linear dynamics may often suffice. In this study, we go beyond performance comparisons to systematically dissect the functional role of nonlinearity in recurrent networks--identifying both when it is computationally necessary, and what mechanisms it enables. We use Almost Linear Recurrent Neural Networks (AL-RNNs), which allow fine-grained control over nonlinearity, as both a flexible modeling tool and a probe into the internal mechanisms of memory. Across a range of classic sequence modeling tasks and a real-world stimulus selection task, we find that minimal nonlinearity is not only sufficient but often optimal, yielding models that are simpler, more robust, and more interpretable than their fully nonlinear or linear counterparts. Our results provide a principled framework for selectively introducing nonlinearity, bridging dynamical systems theory with the functional demands of long-range memory and structured computation in recurrent neural networks, with implications for both artificial and biological neural systems.

A scalable generative model for dynamical system reconstruction from neuroimaging data

Data-driven inference of the generative dynamics underlying a set of observed time series is of growing interest in machine learning and the natural sciences. In neuroscience, such methods promise to alleviate the need to handcraft models based on biophysical principles and allow to automatize the inference of inter-individual differences in brain dynamics. Recent breakthroughs in training techniques for state space models (SSMs) specifically geared toward dynamical systems (DS) reconstruction (DSR) enable to recover the underlying system including its geometrical (attractor) and long-term statistical invariants from even short time series. These techniques are based on control-theoretic ideas, like modern variants of teacher forcing (TF), to ensure stable loss gradient propagation while training. However, as it currently stands, these techniques are not directly applicable to data modalities where current observations depend on an entire history of previous states due to a signal's filtering properties, as common in neuroscience (and physiology more generally). Prominent examples are the blood oxygenation level dependent (BOLD) signal in functional magnetic resonance imaging (fMRI) or Ca$^{2+}$ imaging data. Such types of signals render the SSM's decoder model non-invertible, a requirement for previous TF-based methods. Here, exploiting the recent success of control techniques for training SSMs, we propose a novel algorithm that solves this problem and scales exceptionally well with model dimensionality and filter length. We demonstrate its efficiency in reconstructing dynamical systems, including their state space geometry and long-term temporal properties, from just short BOLD time series.

Learning Interpretable Hierarchical Dynamical Systems Models from Time Series Data

In science, we are often interested in obtaining a generative model of the underlying system dynamics from observed time series. While powerful methods for dynamical systems reconstruction (DSR) exist when data come from a single domain, how to best integrate data from multiple dynamical regimes and leverage it for generalization is still an open question. This becomes particularly important when individual time series are short, and group-level information may help to fill in for gaps in single-domain data. At the same time, averaging is not an option in DSR, as it will wipe out crucial dynamical properties (e.g., limit cycles in one domain vs. chaos in another). Hence, a framework is needed that enables to efficiently harvest group-level (multi-domain) information while retaining all single-domain dynamical characteristics. Here we provide such a hierarchical approach and showcase it on popular DSR benchmarks, as well as on neuroscientific and medical time series. In addition to faithful reconstruction of all individual dynamical regimes, our unsupervised methodology discovers common low-dimensional feature spaces in which datasets with similar dynamics cluster. The features spanning these spaces were further dynamically highly interpretable, surprisingly in often linear relation to control parameters that govern the dynamics of the underlying system. Finally, we illustrate transfer learning and generalization to new parameter regimes.

Multimodal Teacher Forcing for Reconstructing Nonlinear Dynamical Systems

Many, if not most, systems of interest in science are naturally described as nonlinear dynamical systems (DS). Empirically, we commonly access these systems through time series measurements, where often we have time series from different types of data modalities simultaneously. For instance, we may have event counts in addition to some continuous signal. While by now there are many powerful machine learning (ML) tools for integrating different data modalities into predictive models, this has rarely been approached so far from the perspective of uncovering the underlying, data-generating DS (aka DS reconstruction). Recently, sparse teacher forcing (TF) has been suggested as an efficient control-theoretic method for dealing with exploding loss gradients when training ML models on chaotic DS. Here we incorporate this idea into a novel recurrent neural network (RNN) training framework for DS reconstruction based on multimodal variational autoencoders (MVAE). The forcing signal for the RNN is generated by the MVAE which integrates different types of simultaneously given time series data into a joint latent code optimal for DS reconstruction. We show that this training method achieves significantly better reconstructions on multimodal datasets generated from chaotic DS benchmarks than various alternative methods.

Identifying nonlinear dynamical systems from multi-modal time series data

Empirically observed time series in physics, biology, or medicine, are commonly generated by some underlying dynamical system (DS) which is the target of scientific interest. There is an increasing interest to harvest machine learning methods to reconstruct this latent DS in a completely data-driven, unsupervised way. In many areas of science it is common to sample time series observations from many data modalities simultaneously, e.g. electrophysiological and behavioral time series in a typical neuroscience experiment. However, current machine learning tools for reconstructing DSs usually focus on just one data modality. Here we propose a general framework for multi-modal data integration for the purpose of nonlinear DS identification and cross-modal prediction. This framework is based on dynamically interpretable recurrent neural networks as general approximators of nonlinear DSs, coupled to sets of modality-specific decoder models from the class of generalized linear models. Both an expectation-maximization and a variational inference algorithm for model training are advanced and compared. We show on nonlinear DS benchmarks that our algorithms can efficiently compensate for too noisy or missing information in one data channel by exploiting other channels, and demonstrate on experimental neuroscience data how the algorithm learns to link different data domains to the underlying dynamics

Inferring Dynamical Systems with Long-Range Dependencies through Line Attractor Regularization

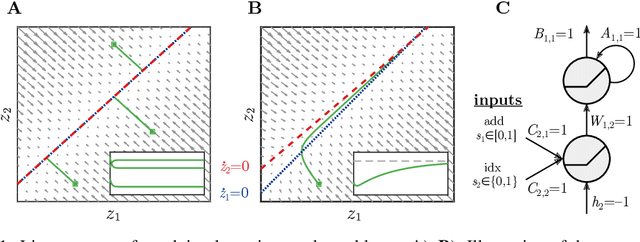
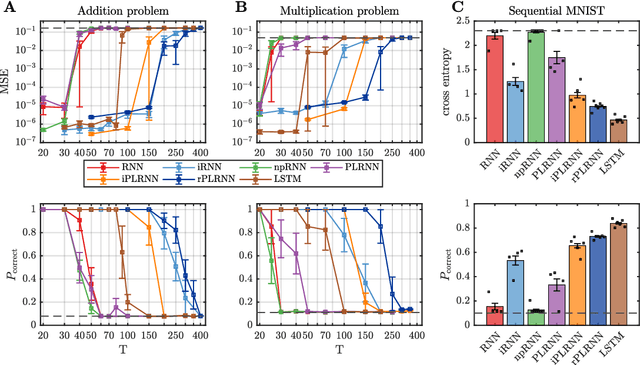
Vanilla RNN with ReLU activation have a simple structure that is amenable to systematic dynamical systems analysis and interpretation, but they suffer from the exploding vs. vanishing gradients problem. Recent attempts to retain this simplicity while alleviating the gradient problem are based on proper initialization schemes or orthogonality/unitary constraints on the RNN's recurrence matrix, which, however, comes with limitations to its expressive power with regards to dynamical systems phenomena like chaos or multi-stability. Here, we instead suggest a regularization scheme that pushes part of the RNN's latent subspace toward a line attractor configuration that enables long short-term memory and arbitrarily slow time scales. We show that our approach excels on a number of benchmarks like the sequential MNIST or multiplication problems, and enables reconstruction of dynamical systems which harbor widely different time scales.

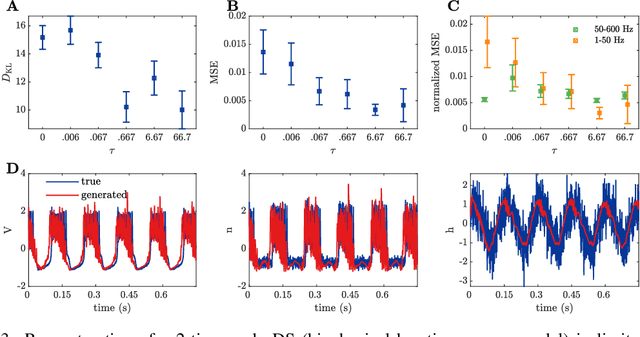
Identifying nonlinear dynamical systems via generative recurrent neural networks with applications to fMRI

A major tenet in theoretical neuroscience is that cognitive and behavioral processes are ultimately implemented in terms of the neural system dynamics. Accordingly, a major aim for the analysis of neurophysiological measurements should lie in the identification of the computational dynamics underlying task processing. Here we advance a state space model (SSM) based on generative piecewise-linear recurrent neural networks (PLRNN) to assess dynamics from neuroimaging data. In contrast to many other nonlinear time series models which have been proposed for reconstructing latent dynamics, our model is easily interpretable in neural terms, amenable to systematic dynamical systems analysis of the resulting set of equations, and can straightforwardly be transformed into an equivalent continuous-time dynamical system. The major contributions of this paper are the introduction of a new observation model suitable for functional magnetic resonance imaging (fMRI) coupled to the latent PLRNN, an efficient stepwise training procedure that forces the latent model to capture the 'true' underlying dynamics rather than just fitting (or predicting) the observations, and of an empirical measure based on the Kullback-Leibler divergence to evaluate from empirical time series how well this goal of approximating the underlying dynamics has been achieved. We validate and illustrate the power of our approach on simulated 'ground-truth' dynamical (benchmark) systems as well as on actual experimental fMRI time series. Given that fMRI is one of the most common techniques for measuring brain activity non-invasively in human subjects, this approach may provide a novel step toward analyzing aberrant (nonlinear) dynamics for clinical assessment or neuroscientific research.