Are Longer Prompts Always Better? Prompt Selection in Large Language Models for Recommendation Systems

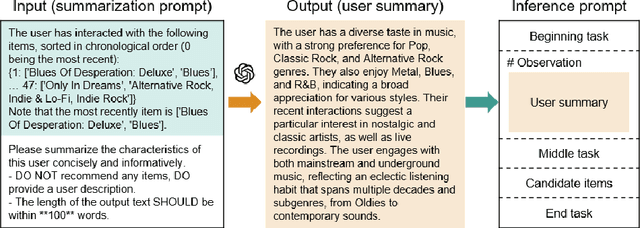
In large language models (LLM)-based recommendation systems (LLM-RSs), accurately predicting user preferences by leveraging the general knowledge of LLMs is possible without requiring extensive training data. By converting recommendation tasks into natural language inputs called prompts, LLM-RSs can efficiently solve issues that have been difficult to address due to data scarcity but are crucial in applications such as cold-start and cross-domain problems. However, when applying this in practice, selecting the prompt that matches tasks and data is essential. Although numerous prompts have been proposed in LLM-RSs and representing the target user in prompts significantly impacts recommendation accuracy, there are still no clear guidelines for selecting specific prompts. In this paper, we categorize and analyze prompts from previous research to establish practical prompt selection guidelines. Through 450 experiments with 90 prompts and five real-world datasets, we examined the relationship between prompts and dataset characteristics in recommendation accuracy. We found that no single prompt consistently outperforms others; thus, selecting prompts on the basis of dataset characteristics is crucial. Here, we propose a prompt selection method that achieves higher accuracy with minimal validation data. Because increasing the number of prompts to explore raises costs, we also introduce a cost-efficient strategy using high-performance and cost-efficient LLMs, significantly reducing exploration costs while maintaining high prediction accuracy. Our work offers valuable insights into the prompt selection, advancing accurate and efficient LLM-RSs.

Kernel method for persistence diagrams via kernel embedding and weight factor

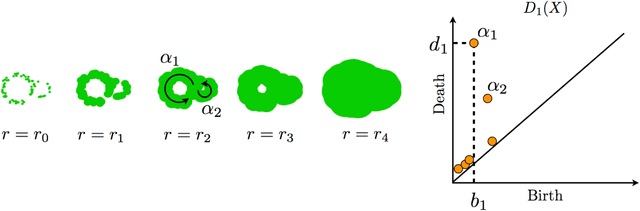
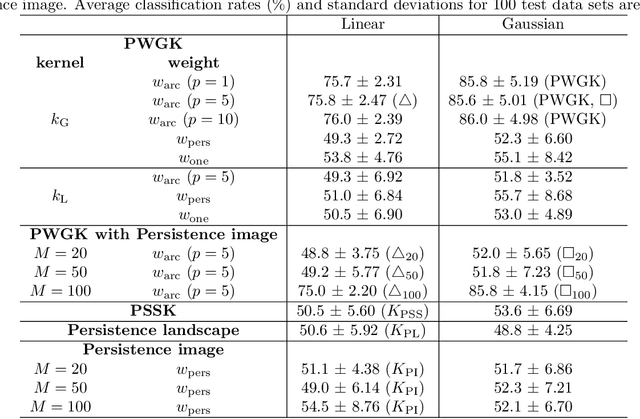
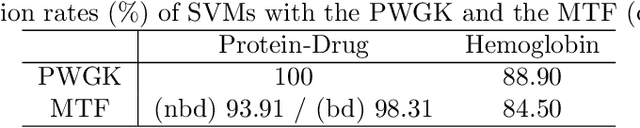
Topological data analysis is an emerging mathematical concept for characterizing shapes in multi-scale data. In this field, persistence diagrams are widely used as a descriptor of the input data, and can distinguish robust and noisy topological properties. Nowadays, it is highly desired to develop a statistical framework on persistence diagrams to deal with practical data. This paper proposes a kernel method on persistence diagrams. A theoretical contribution of our method is that the proposed kernel allows one to control the effect of persistence, and, if necessary, noisy topological properties can be discounted in data analysis. Furthermore, the method provides a fast approximation technique. The method is applied into several problems including practical data in physics, and the results show the advantage compared to the existing kernel method on persistence diagrams.