Convergence Rates for Distribution Matching with Sliced Optimal Transport

We study the slice-matching scheme, an efficient iterative method for distribution matching based on sliced optimal transport. We investigate convergence to the target distribution and derive quantitative non-asymptotic rates. To this end, we establish __ojasiewicz-type inequalities for the Sliced-Wasserstein objective. A key challenge is to control along the trajectory the constants in these inequalities. We show that this becomes tractable for Gaussian distributions. Specifically, eigenvalues are controlled when matching along random orthonormal bases at each iteration. We complement our theory with numerical experiments and illustrate the predicted dependence on dimension and step-size, as well as the stabilizing effect of orthonormal-basis sampling.

Optimal Transport-based Conformal Prediction

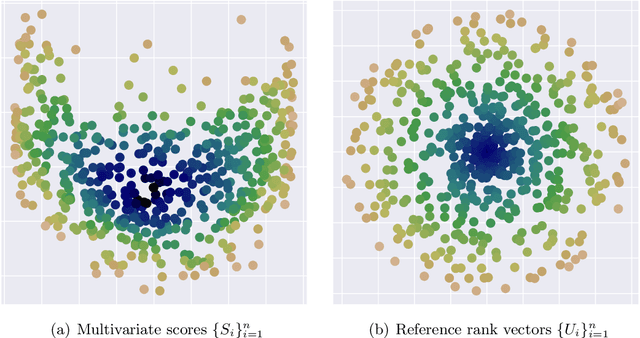
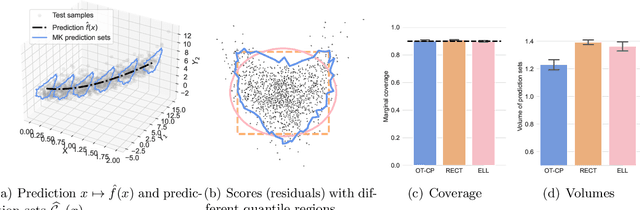
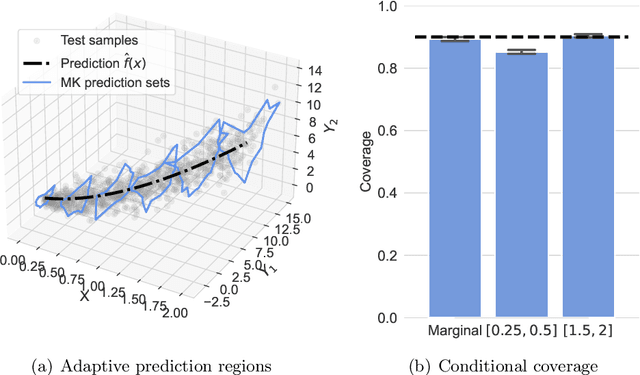
Conformal Prediction (CP) is a principled framework for quantifying uncertainty in blackbox learning models, by constructing prediction sets with finite-sample coverage guarantees. Traditional approaches rely on scalar nonconformity scores, which fail to fully exploit the geometric structure of multivariate outputs, such as in multi-output regression or multiclass classification. Recent methods addressing this limitation impose predefined convex shapes for the prediction sets, potentially misaligning with the intrinsic data geometry. We introduce a novel CP procedure handling multivariate score functions through the lens of optimal transport. Specifically, we leverage Monge-Kantorovich vector ranks and quantiles to construct prediction region with flexible, potentially non-convex shapes, better suited to the complex uncertainty patterns encountered in multivariate learning tasks. We prove that our approach ensures finite-sample, distribution-free coverage properties, similar to typical CP methods. We then adapt our method for multi-output regression and multiclass classification, and also propose simple adjustments to generate adaptive prediction regions with asymptotic conditional coverage guarantees. Finally, we evaluate our method on practical regression and classification problems, illustrating its advantages in terms of (conditional) coverage and efficiency.

Stochastic optimal transport in Banach Spaces for regularized estimation of multivariate quantiles

We introduce a new stochastic algorithm for solving entropic optimal transport (EOT) between two absolutely continuous probability measures $\mu$ and $\nu$. Our work is motivated by the specific setting of Monge-Kantorovich quantiles where the source measure $\mu$ is either the uniform distribution on the unit hypercube or the spherical uniform distribution. Using the knowledge of the source measure, we propose to parametrize a Kantorovich dual potential by its Fourier coefficients. In this way, each iteration of our stochastic algorithm reduces to two Fourier transforms that enables us to make use of the Fast Fourier Transform (FFT) in order to implement a fast numerical method to solve EOT. We study the almost sure convergence of our stochastic algorithm that takes its values in an infinite-dimensional Banach space. Then, using numerical experiments, we illustrate the performances of our approach on the computation of regularized Monge-Kantorovich quantiles. In particular, we investigate the potential benefits of entropic regularization for the smooth estimation of multivariate quantiles using data sampled from the target measure $\nu$.