Capturing functional connectomics using Riemannian partial least squares

For neurological disorders and diseases, functional and anatomical connectomes of the human brain can be used to better inform targeted interventions and treatment strategies. Functional magnetic resonance imaging (fMRI) is a non-invasive neuroimaging technique that captures spatio-temporal brain function through blood flow over time. FMRI can be used to study the functional connectome through the functional connectivity matrix; that is, Pearson's correlation matrix between time series from the regions of interest of an fMRI image. One approach to analysing functional connectivity is using partial least squares (PLS), a multivariate regression technique designed for high-dimensional predictor data. However, analysing functional connectivity with PLS ignores a key property of the functional connectivity matrix; namely, these matrices are positive definite. To account for this, we introduce a generalisation of PLS to Riemannian manifolds, called R-PLS, and apply it to symmetric positive definite matrices with the affine invariant geometry. We apply R-PLS to two functional imaging datasets: COBRE, which investigates functional differences between schizophrenic patients and healthy controls, and; ABIDE, which compares people with autism spectrum disorder and neurotypical controls. Using the variable importance in the projection statistic on the results of R-PLS, we identify key functional connections in each dataset that are well represented in the literature. Given the generality of R-PLS, this method has potential to open up new avenues for multi-model imaging analysis linking structural and functional connectomics.

Em-K Indexing for Approximate Query Matching in Large-scale ER

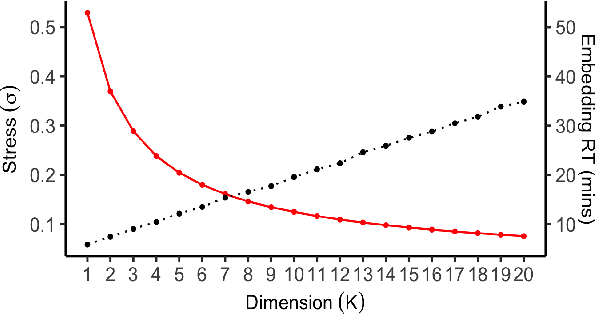
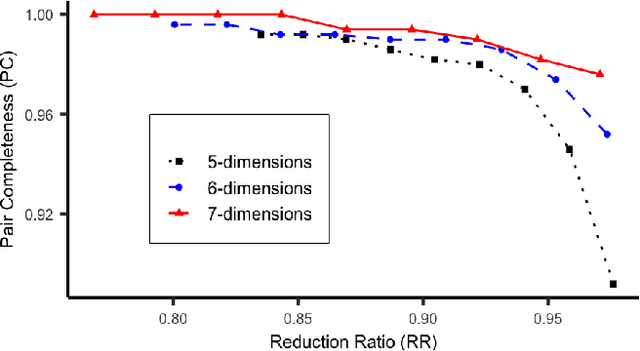
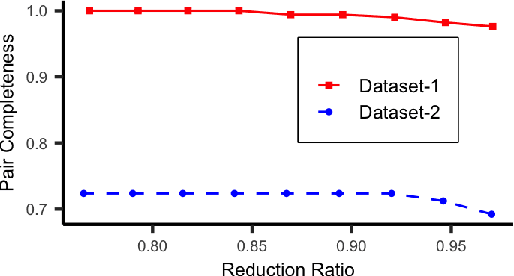
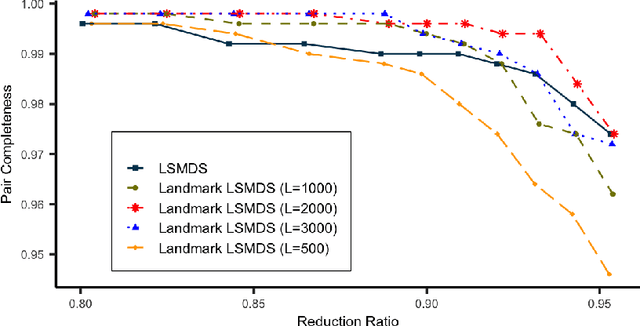
Accurate and efficient entity resolution (ER) is a significant challenge in many data mining and analysis projects requiring integrating and processing massive data collections. It is becoming increasingly important in real-world applications to develop ER solutions that produce prompt responses for entity queries on large-scale databases. Some of these applications demand entity query matching against large-scale reference databases within a short time. We define this as the query matching problem in ER in this work. Indexing or blocking techniques reduce the search space and execution time in the ER process. However, approximate indexing techniques that scale to very large-scale datasets remain open to research. In this paper, we investigate the query matching problem in ER to propose an indexing method suitable for approximate and efficient query matching. We first use spatial mappings to embed records in a multidimensional Euclidean space that preserves the domain-specific similarity. Among the various mapping techniques, we choose multidimensional scaling. Then using a Kd-tree and the nearest neighbour search, the method returns a block of records that includes potential matches for a query. Our method can process queries against a large-scale dataset using only a fraction of the data $L$ (given the dataset size is $N$), with a $O(L^2)$ complexity where $L \ll N$. The experiments conducted on several datasets showed the effectiveness of the proposed method.

High Performance Out-of-sample Embedding Techniques for Multidimensional Scaling

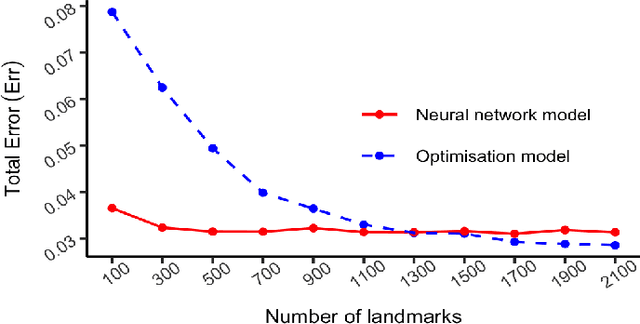
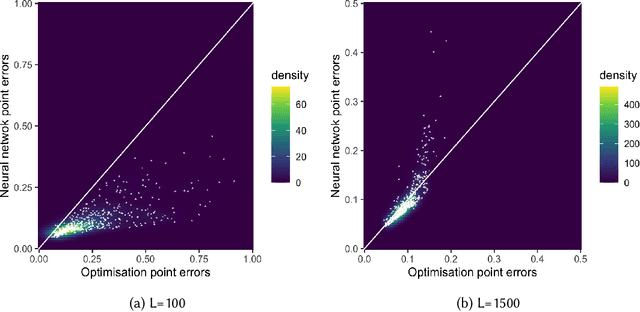
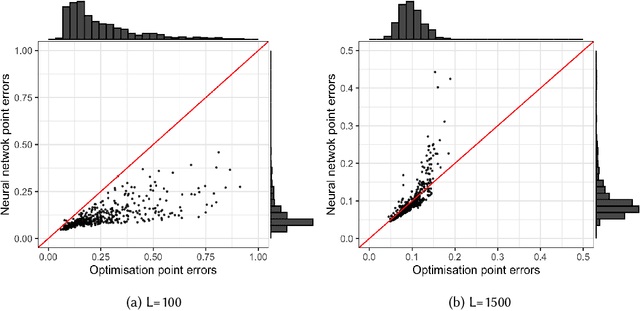
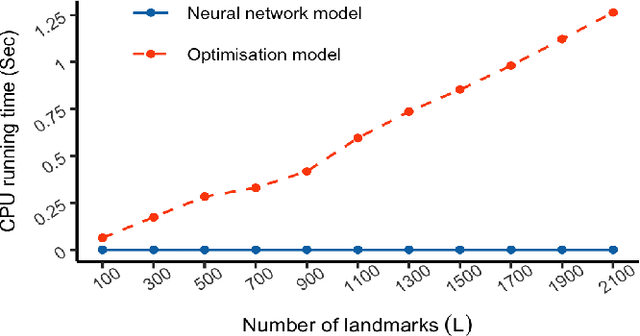
The recent rapid growth of the dimension of many datasets means that many approaches to dimension reduction (DR) have gained significant attention. High-performance DR algorithms are required to make data analysis feasible for big and fast data sets. However, many traditional DR techniques are challenged by truly large data sets. In particular multidimensional scaling (MDS) does not scale well. MDS is a popular group of DR techniques because it can perform DR on data where the only input is a dissimilarity function. However, common approaches are at least quadratic in memory and computation and, hence, prohibitive for large-scale data. We propose an out-of-sample embedding (OSE) solution to extend the MDS algorithm for large-scale data utilising the embedding of only a subset of the given data. We present two OSE techniques: the first based on an optimisation approach and the second based on a neural network model. With a minor trade-off in the approximation, the out-of-sample techniques can process large-scale data with reasonable computation and memory requirements. While both methods perform well, the neural network model outperforms the optimisation approach of the OSE solution in terms of efficiency. OSE has the dual benefit that it allows fast DR on streaming datasets as well as static databases.